Курсовая работа: Контроль и диагностика систем

Р⁽⁴⁾ = (р₁ (5)/р₁ (4)) Р⁽³⁾ = 0.98495

Р⁽⁵⁾ = (р₁ (6)/р₁ (5)) Р⁽⁴⁾ = 0.98519

Р⁽⁶⁾ = (р₂ (2)/р₂ (1)) Р⁽⁵⁾ = 0.98658

Р⁽⁷⁾ = (р₁ (7)/р₁ (6)) Р⁽⁶⁾ = 0.98679

Р⁽⁸⁾ = (р₁ (8)/р₁ (7)) Р⁽⁷⁾ = 0.98696

Р⁽⁹⁾ = (р₅ (2)/р₅ (1)) Р⁽⁸⁾ = 0.98944

Р⁽¹⁰⁾ = (р₃ (2)/р₃ (1)) Р⁽⁹⁾ = 0.99018

Р⁽¹¹⁾ = (р₂ (3)/р₂ (2)) Р⁽¹⁰⁾ = 0.99064

Р⁽¹²⁾ = (р₂ (4)/р₂ (3)) Р⁽¹¹⁾ = 0.99089

Р⁽¹³⁾ = (р₁ (9)/р₁ (8)) Р⁽¹²⁾ = 0.99099

Р⁽¹⁴⁾ = (р₁ (10)/р₁ (9)) Р⁽¹³⁾ = 0.99110

Р⁽¹⁵⁾ = (р₁ (11)/р₁ (10)) Р⁽¹⁴⁾ = 0.99119

Р⁽¹⁶⁾ = (р₂ (5)/р₂ (4)) Р⁽¹⁵⁾ = 0.99141

Р⁽¹⁷⁾ = (р₂ (6)/р₂ (5)) Р⁽¹⁶⁾ = 0.99152

Р⁽¹⁸⁾ = (р₂ (7)/р₂ (6)) Р⁽¹⁷⁾ = 0.99163

Р⁽¹⁹⁾ = (р₁ (12)/р₁ (11)) Р⁽¹⁸⁾ = 0.99169

Р⁽²⁰⁾ = (р₄ (2)/р₄ (1)) Р⁽¹⁹⁾ = 0.99206

Р⁽²¹⁾ = (р₃ (3)/р₃ (2)) Р⁽²⁰⁾ = 0.99233

Р⁽²²⁾ = (р₂ (8)/р₂ (7)) Р⁽²¹⁾ = 0.99238

Полученные результаты занесем в таблицу:

Таблица 2.5

N	n1	n2	n3	n4	n5	Р( N )	Т( N )
1	2	1	1	1	1	0.98275	1 мин 36 с
2	3	1	1	1	1	0.98398	1 мин 39 с
3	4	1	1	1	1	0.98454	1 мин 42 с
4	5	1	1	1	1	0.98495	1 мин 45 с
5	6	1	1	1	1	0.98519	1 мин 48 с
6	6	2	1	1	1	0.98658	1 мин 53 с
7	7	2	1	1	1	0.98679	1 мин 56 с
8	8	2	1	1	1	0.98696	1 мин 59 с
9	8	2	1	1	2	0.98944	2 мин 49 с
10	8	2	2	1	2	0.99018	3 мин 4 с
11	8	3	2	1	2	0.99064	3 мин 9 с
12	8	4	2	1	2	0.99089	3 мин 14 с
13	9	4	2	1	2	0.99099	3 мин 17 с
14	10	4	2	1	2	0.99110	3 мин 20 с
15	11	4	2	1	2	0.99119	3 мин 23 с
16	11	5	2	1	2	0.99141	3 мин 28 с
17	11	6	2	1	2	0.99152	3 мин 33 с
18	11	7	2	1	2	0.99163	3 мин 38 с
19	12	7	2	1	2	0.99169	3 мин 41 с
20	12	7	2	2	2	0.99206	4 мин 1 с
21	12	7	3	2	2	0.99233	4 мин 16 с
22	12	8	3	2	2	0.99238	4 мин 21 с
23	12	8	3	2	3	0.99317	5 мин 11 с
Далее производить расчет нецелесообразно, т.к. решение задачи найдено

Оптимальное решение задачи – n₁ = 12, n₂ = 8, n₃ = 3, n₄ = 2, n₅ = 2, где Т = 4мин 21 с, при этом максимальная достоверность результатов равна 0.99238 ( в таблице2.5. оптимальное решение этой задачи выделено голубым цветом)

Программная часть

Задача №1

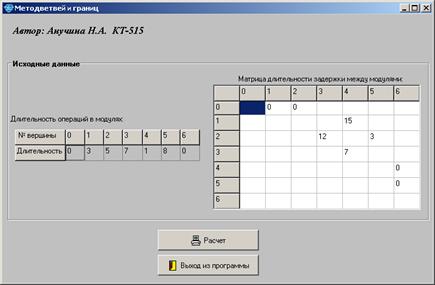
рис.3.1. Интерфейс программы

В данное окно вводятся исходные данные. При нажатии кнопки «Расчет» начинаем расчет. В итоге получаем следующее окно.

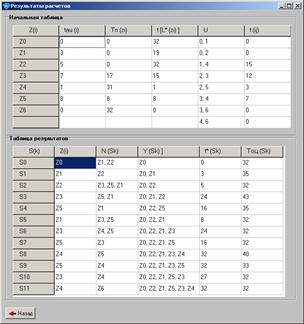
рис. 3.2. Результат расчета

В верхней таблице «Начальная таблица» приведены значения наиболее ранних времен начала модулей Z_i и длины критических путей.

В нижней таблице «Таблица результатов» приведены результаты расчета.