Курсовая работа: Контроль и диагностика систем

T_оц (S₉ ) = 17 + max{15 + max(0,17-17)} = 32

T_оц (S₁₅ ) = 32 + max{8 + max(0,7-32)} = 40

T_оц (S₁₆ ) = 30+ max{3+ max(0,29-30)} = 33

T_оц (S₁₇ ) = 22 + max{3 + max(0,29-22)} = 32

T_оц (S₂₆ ) = 32 + max{0 + max(0,32-32)} = 32

Таблица 1.4.

S	Zi /i = Sk	N(Sk )	Y(Sk )	t*(Sk )	Tоц (Sk )
S0	Z0	Z1 Z2	Z0	0	32
S1	Z1	Z2 Z3	Z0 Z1	2	32
S2	Z2	Z5 Z1	Z0 Z2	4	36
S3	Z3	Z2	Z0 Z1 Z3	22	41
S4	Z2	Z5 Z3	Z0 Z1 Z2	6	32
S8	Z3	Z4 Z5	Z0 Z1 Z2 Z3	22	32
S9	Z5	Z3	Z0 Z1 Z2 Z5	17	32
S15	Z3	Z5	Z0 Z1 Z2 Z3 Z4	32	40
S16	Z5	Z4	Z0 Z1 Z2 Z3 Z5	30	33
S17	Z5	Z4	Z0 Z1 Z2 Z5 Z3	22	32
S 26	Z1	Z 6	Z0 Z1 Z2 Z 5 Z 3 Z4	32	32

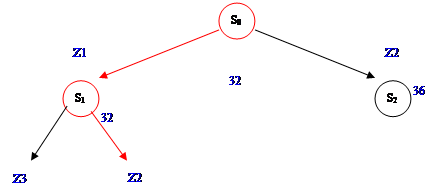
Составим дерево оптимального решения (рис 1.3)

Рис1.3 - Дерево оптимального решения

Таким образом получили, что оптимальному процессу контроля соответствует последовательность проверок {Z ₀ Z ₁ Z ₂ Z ₅ Z ₃ Z ₄ }, при этом общее время контроля составляет Т_опт = 32 ед.

Задача №2

Дано: Характеристики параметров, допуски и погрешность измерений.

Таблица 2.1

№ параметра	1	2	3	4	5
σИЗМ /σПАР	0.5	0.3	0.2	0.1	0.4
ti	3	5	15	20	50

Найти: обеспечить максимально возможную достоверность результатов контроля при условии, что суммарное время измерения контролируемых параметров не превысит заданной величины:

- суммарное время измерения контролируемых параметров не должно превышать 5 мин.

Решение:

1. Для каждого параметра определим значение p_i (n_i ):

Таблица 2.2

n	σИЗМ /σПАР
	0.5	0.3	0.2	0.1	0.4
1	0.99110	0.99634	0.99784	0.99893	0.99419
2	0.99533	0.99775	0.99859	0.99930	0.99669
3	0.99657	0.99821	0.99886	0.99945	0.99748
4	0.99714	0.99846	0.99901	0.99955	0.99785
5	0.99756	0.99868	0.99915	0.99960	0.99816
6	0.99780	0.99879	0.99923	0.99963	0.99833
7	0.99801	0.99890	0.99931	0.99967	0.99849
8	0.99818	0.99895	0.99933	0.99970	0.999859
9	0.99828	0.99901	0.99937	0.99971	0.99867
10	0.99839	0.99909	0.99942	0.99973	0.99876
11	0.99848	0.99914	0.99945	0.99974	0.99882
12	0.99854	0.99918	0.99948	0.99975	0.99887

2. Для каждого значения параметра вычисляются значения y_i (n_i ) выбирается наибольшее значение:

3.

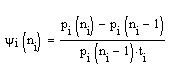
y₁ (n_i )

y₁ (2) = (0.99533-0.99110)/0.99110*3 = 0.001422661

y₁ (3) = 0.000415272

y₁ (4) = 0.000190653

y₁ (5) = 0.000140401

y₁ (6) = 0.000718243

y₁ (7) = 0.000070154

y₁ (8) = 0.000056779

y₁ (9) = 0.000033394