Курсовая работа: Механізм важіля

7,629² *0,291=16,937мс^-1 ,

an₂ =/ μ_a =9,678мм.

Вектор - тангенциальне прискорення точки В відносно точки А, яке має напрямок перпендикулярний нормальному, але модуль його невідомий.

Вектор - нормальне прискорення точки В відносно точки О₂ , яке має напрямок від точки В до точки О₂ .

=51,01мс^-2 ,

πn₃ =/μ_a =29,149мм.

З точки n ₂ проведемо лінію у напрямку вектора до пересічення з лінією, проведеною з точки n ₃ у напрямку вектора . Точку пересічення позначемо b і з’єднаємо її з полюсом π .

Величини тангенціальних прискорень:

=n ₂ b *μ_a =87,84*1,75=152,95 мс^-2 ,

=n ₃ b *μ_a =81,4*1,75=142,45мс^-2 .

Кутові прискорення ланок:

ε₂ =/l_AB =525,6 рад/с² ,

ε₃ =/l_{BO 2} =614 рад/с² .

Напрямки кутових прискорень показані на креслені (див. арк. 2).

Прискорення точки С знайдемо, базуючись на теорему подібності, з пропорції

; Звідси

=0,29*86,46/0,232=108,075 мм.

=108,075*1,75 = 189,13мс^-2

Прискорення точки Д визначимо, вирішивши графічно векторне рівняння:

Тут вектор - нормальне прискорення точки Д у відносному русі навколо точки С. Цей вектор напрямлений від точки Д до точки С.

=4,734² *0,319=7,149 мс^-2

- тангенційне прискорення точки Д відносно точки С.

З точки с плану прискорення у напрямку вектора проводимо промінь, на якому відкладаємо

cn ₄ =/μ_a =7,149/1,75=4,085 мм.

З точки n ₄ проведемо лінію, перпендикулярну ланці СД, до пересічення з лінією, проведеною з полюса π паралельно вісі х₁ -х₁ . Точку пересічення позначемо д .

а_Д =πд *μ_а =112,14*1,75=196,245 мс^-2 .

=n ₄ д * μ_а =1,69*1,75=2,958мс^-2 .

Кутове прискорення ланки 4

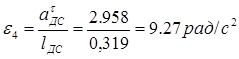
Положення центрів ваги на плані прискорень показуємо на серединах відрізків повних відносних прискорень.

Прискорення центрів ваги:

а_{s 2} =πS₂ *μ_a =95,42*1,75=166,985мс^-2 ,

а_{s 3} =πS₃ *μ_a =54*1,75=94,5мс^-2 ,

а_{s 4} =πS₄ *μ_a =109,72*1,75=192,01мс^-2 .

а_{s 5} = a_Д =196,245 мс^-2