Курсовая работа: Методи розв’язування раціональних нерівностей вищих степенів

Отже числа,, є коренями даного рівняння. Наносимо ці числа на числову вісь і визначаємо знак лівої частини функції

на одному з інтервалів. Зокрема, взявши точку з інтервалу , дістаємо . Провівши «криву знаків», визначаємо знак в кожному з інтервалів.

+ +

1 2 3 x

Відповідь:

2.2 Розв’язування раціональних нерівностей вищих степенів узагальненним методом інтервалів

Нехай потрібно розв'язати нерівність

,

де цілі додатні числа;

— дійсні числа, серед яких немає рівних і такі, що . Нерівності подібного типу розв'язують із застосуванням узагальненого метода інтервалів. В основі цього метода лежить така властивість двочлена точка ділить числову вісь на дві частини, причому якщо (- парне), то вираз праворуч і ліворуч від точки зберігає додатний знак; якщо (- непарне число), то вираз праворуч від точки додатний, а ліворуч від точки від'ємний.

Для розв'язання нерівності

узагальненим методом інтервалів на числову вісь наносимо числа ; в проміжку праворуч від найбільшого з них ставимо знак «плюс», а потім, рухаючись справа наліво, при переході через чергове число змінюємо знак, якщо — непарне число, і зберігаємо знак, якщо. — парне число.

Зауваження 1. Якщо зустрічаються вирази , то праворуч від найбільшого з не обов'язково буде знак « + ». У цьому випадку найкраще визначити знак лівої частини нерівності в якомусь з інтервалів, а потім поставити знаки в кожному з інтервалів з урахуванням викладених вище міркувань.

Зауваження 2.Наведені вище міркування справедливі і для нерівностей виду

, , , де

.

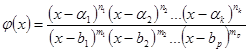Приклад 1. Розв’язати нерівність

Перепишемо нерівність у рівносильному вигляді

Числа , , , є коренями рівняння. Наносимо ці числа на числову вісь і визначаємо знак лівої частини функції

на одному з інтервалів. Зокрема, взявши точку з інтервалу , дістаємо . Проводимо через задані точки «криву знаків» з урахуванням того, що ліворуч і праворуч точки буде той самий знак «+», тому що у виразі показник степеня (число 4) є числом парним.