Курсовая работа: Методи розв’язування раціональних нерівностей вищих степенів

Відповідь:.

2.3 Розв’язування дробово-раціональних нерівностей

Приклад 1. Розв’язати нерівність

.

Розв’язання: розкладемо чисельник і знаменник дробу, що стоїть в лівій частині нерівності, на множники:

.

Отриманий дріб містить два нелінійні множники: і . Перший з них додатний і його можна опустити, другий множник виключимо у відповідності з пунктом 4:

Далі, на числовій осі відмітимо точки , та інтервали, що утворюються при цьому, знаками:

+ +

-2 2 x

Виберемо інтервал відмічений знаком «-» (так як ), і нанесемо на числову вісь точку . Ця точка попадає у вибраний інтервал. «Виколюючи» точку , отримуємо інтервали і , об’єднання яких утворює множину розв’язків даної нерівності:

Відповідь: .

Приклад 2 . Розв’язати нерівність

.

Розв’язання: розкладемо багаточлен, що стоїть в чисельнику лівої частини нерівності, на множники. Розглянемо рівняння . Серед дільників 8 підберемо корінь рівняння . Розділимо ліву частину рівняння на двочлен :

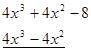
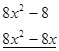
Тепер розглянемо рівняння . Серед дільників 8 підберемо рівняння і розділимо ліву частину на двочлен :

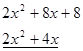
Так як квадратний тричлен не має дійсних коренів, отримаємо розкладення