Курсовая работа: Методи розв’язування раціональних нерівностей вищих степенів

Таким чином, дана нерівність перетворюється до вигляду:

.

Дріб в лівій частині цієї нерівності містить два нелінійних множники: квадратний тричлен , що більший нуля, і . Виключимо ці множники:

На числовій осі відмітимо точки , і інтервали, що утворюються знаками:

Виберемо інтервал зі знаком «-» і потім відмітимо на осі точку . Ця точка належить вибраному інтервалу, і тому, виключаючи цю точку, отримуємо, що - множина розв’язків даної нерівності.

Відповідь: .

Приклад 3. Розв’язати нерівність

.

Розв’язання: у відповідності з описаною схемою методу інтервалів

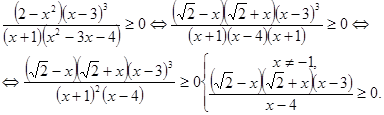
Будемо відмічати на числовій осі точки , , зафарбованими кружками (нерівність нестрога!), а точку - світлим кружком:

Розв’язок даної даної нерівності складаються з об’єднанням проміжків .

Відповідь: .

Приклад 4. Розв’язати нерівність

.

Розв’язування: Нанасимо на числову пряму точки , , , , . Точки , , відзначаємо темними кружками, а точки , світлими.

Провівши «кривину знаків» з урахуванням того, що в околі точок і ліва частина нерівності зберігає знак (тому що у виразах ), показники степенів є парними числами), дістанемо розв’язання Ця множина на рисунку заштрихована.

Відповідь:

Приклад 5. Розв’язати нерівність

.

Наносимо точки числову вісь. За допомогою «кривої знаків» дістанемо розв’язки, заштриховані на рисунку.

Зазначимо, що точка входить у множину розв’язків, тому що при дістанемо .

Відповідь: .

2.4 Розв’язування раціональних нерівностей методом заміни змінної