Курсовая работа: Многомерная геометрия 2

i = 1,…, k ; = - 1, если i = k + 1,…, n . Тем самым векторы базиса нормированы так, что квадраты их норм по модулю равны единице. Векторы e _i называются единичными, если i k , мнимоединичным, если i k + 1. Вообще вектор a называется единичным, если мнимоединичным, если .

Определение. Базис e ₁ ,…, e_n , удовлетворяющий перечисленным в этом пункте условиям, называется ортонормированным.

Теорема 1. В n – мерном линейном пространстве с заданной квадратичной метрикой всякий набор из попарно ортогональных единичных или мнимоединичных векторов общим числом n является базисом, в котором метрическая форма имеет нормальный вид.

Доказательство. Пусть e ₁ ,…, e_n – указанный набор векторов. Убедимся, что они линейно независимы. Рассмотрим соотношение

₁ e ₁ +

Отсюда, умножая скалярно наe ₁ , получим

Но по условию ( e ₁ , e ₁ ) = 1, ( e _j , e ₁ ) = 0 ( j 1); кроме того, (, e ₁ ) = 0 . Следовательно, = 0. Аналогично докажем, что векторы e ₁ ,…, e_n независимы и, значит, действительно составляют базис.

Так как g ( e _i , e _i ) = ( e _i , e _i ) = 1 g ( e _i , e _i )= ( e _i , e _i )=0, то форма g ( e _i , e _i ) в базисе e ₁ ,…, e_n имеет нормальный вид.

2. Наряду с доказанной выше теоремой 1 мы отметим следующее утверждение.

В n – мерном линейном пространстве всегда можно задать, причем единственным способом, такую квадратичную метрику, что произвольный заранее данный базис e ₁ ,…, e _k , e _k + 1,…, e_n станет ортонормированным, его векторы e ₁ ,…, e _k станут единичными, а векторы e _k + 1,…, e_n – мнимо- единичными; здесь k – также любое заранее данное целое число от 0 доn .

Доказательство. Искомая метрика однозначно определяется заданием метрической формы g ( x , x ) которая в базисе e ₁ ,…, e _k , e _k + 1,…, e_n имеет вид

g(x, x) = (x¹ )² +…+(x ^k )² – (x ^{k+ 1} )² - …- (x ⁿ )² .

3. Согласно закону инерции квадратичных форм число единичных и число мнимо-единичных векторов не зависит от выбора базиса, ортонормированного в данной квадратичной метрике.

Определение. Числи k единичных векторов ортонормированного базиса называется положительным индексом пространства с данной квадратичной метрикой.

Если k = n или еслиk = 0, то пространство называется евклидовым .

Если 1 k n – 1 , то пространство называется псевдоевклидовым .

Особенно большое значение имеет псевдоевклидово пространство при

k = n – 1 . Оно называется пространством Минковского и при n = 4 играет важную роль в теории относительности.

1.4.Ортогональная проекция. Ортогонализация

1. В этом параграфе рассмотрим евклидово пространство L, то есть линейное пространство со знакоопределенной метрической формой.

Будем считать метрическую форму положительно определенной.

Размерность пространства L может быть бесконечной.

Пусть в L дано подпространство . Допустим, что вектор x L представляется в виде суммы

= (1)

где , а ортогонален к . Тогда вектор называется ортогональной проекцией вектора x на подпространство. Ортогональная проекция вектора x на единственна. В самом деле пусть имеется другое разложение где ортогонален к . В этом случае отсюда так как а и ортогональны к . Из следует, что то есть поскольку метрическая форма пространства положительно определена.

Частный случай. Когда L трехмерно двумерно, показан на рис. 1.

Преобразование пространства L , которое каждому вектору x ставит в соответствии вектор согласно формуле (1), тоже называется ортогональной проекцией на .

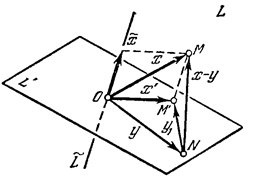Если пространство L рассматривается как точечное, то а - как плоскость в нем, то точка с радиус – вектором называется ортогональной проекцией на L точки M на представляет собой

Рис. 1