Курсовая работа: Многомерная геометрия 2

Соответственно

(13)

Следует определить внимание на ее положительную определенность: , причем тогда и только тогда, когда непрерывная функция во всех точках отрезка.

Возьмем систему одночленов

(14)

и причем к ней процесс ортогонализации. В результате получим последовательность многочленов

(15)

Номера многочленов (15) выбраны так, чтобы они совпадали с их степенями. Коэффициенты многочленов вычисляются согласно формулам (9) с учетом (10), (11), (12) и (14).

После специальной нормировки вида

где выбираются из условия

(16)

Получаем последовательность многочленов называемых многочленами Лежандра. Можно доказать, что

(17)

Учитывая замечание в п. 6, для этого достаточно проверить, что все многочлены (17) попарно ортогональны и что они удовлетворяют условию (16).

Можно доказать также, что

Таким образом, система многочленов Лежандра ортогональна, но не нормирована.

Рис.1

Глава II. Аффинные преобразования

2.1 . Аффинные преобразования на плоскости

В компьютерной графике все, что относится к двумерному случаю принято обозначать символом (2D) (2-dimention).

Допустим, что на плоскости введена прямолинейная координатная система. Тогда каждой точке М ставится в соответствие упорядоченная пара чисел (х, у) ее координат (рис. 5). Вводя на плоскости еще одну прямолинейную систему координат, мы ставим в соответствие той же точке М другую пару чисел – (x^* , y^* ).

0

Y

X

M (x, y)

Рис.5

Переход от одной прямолинейной координатной системы на плоскости к другой описывается следующими соотношениями:

x^* =ax+ by +l, (2.1)

y^* =gx+ by + m, (2.2)

где a, b, g, l, m -- произвольные числа, связанные неравенством:

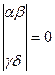(2.3)

Формулы (2.1) и (2.2) можно рассматривать двояко: либо сохраняется точка и изменяется координатная система (рис. 6) – в этом случае произвольная точка М остается той же, изменяются лишь ее координаты (х, у) | (х^* , y^* ), либо изменяется точка и сохраняется ко?