Курсовая работа: Обработка статистической информации при определении показателей надежности

Первый способ проверки информации на выпадающие точки заключается в

проверке по правилу . Так как, при законе нормального распределения 99,7% всех точек находятся в интервале , то все точки, входящие в этот интервал, считаются действительными.

Для рассматриваемого примера границы достоверности точек информации будут соответственно равны:

нижняя граница:

верхняя граница:

Наименьший размер толщины шлиц первичного вала , что больше , следовательно, первая точка информации достоверна и должна учитываться при дальнейших расчетах.

Наибольший размер толщины шлиц первичного вала , что меньше , следовательно, последняя точка информации достоверна и должна учитываться при дальнейших расчетах.

Второй способ проверки достоверности точек производится по критерию l (критерий Ирвина). Этот способ является более точным. При этом определяется опытное значение критерия lоп по формуле:

, (1.5)

где ti+1, ti – смежные точки информации , и сравниваются с нормированным значением l.

Если λоп < λ точка достоверна;

λоп > λ точка недостоверна.

Проведя проверку крайних точек информации по доремонтным ресурсам толщины зуба третьей передачи, получим

для наименьшей точки информации ()

;

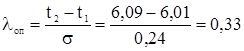для наибольшей точки информации ()

.

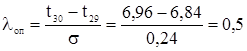Для объема информации N=30 и доверительной вероятности α=0,95 нормированное значение критерия λ=1,2.

Сравнение опытных значений критерия Ирвина с нормированным его значением показывает, что первая точка информации является достоверной, λоп =0,16 < λ=1,2 и её следует учитывать в дальнейших расчетах. Последняя точка информации также является достоверной, λоп =0,32 < λ=1,2 и её тоже следует учитывать в дальнейших расчетах.

В случаях, когда исключаются выпадающие точки, нужно перестроить статистический ряд и пересчитать среднее значение и среднее квадратическое отклонение показателя надежности.

1.4 Графическое изображения опытного распределения

По данным статистического ряда могут быть построены полигон и кривая накопленных опытных вероятностей (рисунки 1.1 и 1.2 в приложении), которые дают наглядное представление об опытном распределении показателя надежности.

При выборе масштаба при построении графиков желательно придерживаться правила «золотого сечения», т.е.

, (1.6)

где y – максимальное значение ординаты;

x – максимальное значение абсциссы.

При построении полигона распределения по оси абсцисс откладывают в определенном масштабе показатель надежности t, а по оси ординат - опытную частоту mi или опытную вероятность Pi.

Для построения кривой накопленных опытных вероятностей по оси абсцисс откладывают в масштабе значения показателя надежности t, а по оси ординат – накопленную опытную вероятность ∑ Pi.

Точки полигона образуются пересечением ординаты, равной опытной вероятности интервала, и абсциссы, равной середине этого интервала. Точки кривой накопленных опытных вероятностей образуются пересечением ординаты, равной сумме опытных вероятностей и абсциссы - конца данного интервала.