Курсовая работа: Обработка статистической информации при определении показателей надежности

; (1.29)

, (1.30)

где - нижняя доверительная граница одиночного значения показателя надежности;

- верхняя доверительная граница одиночного значения показателя надежности;

σ – среднее квадратическое отклонение;

- коэффициент Стьюдента определяется по таблице в зависимости от принятой доверительной вероятности α и объема информации N;

- доверительный интервал;

- абсолютная ошибка рассеивания.

б) для среднего значения показателя надежности:

; (1.31)

; (1.32)

; (1.33)

, (1.34)

где - - нижняя доверительная граница рассеивания среднего значения показателя надежности;

- верхняя доверительная граница рассеивания среднего значения показателя надежности;

- абсолютная ошибка рассеивания среднего значения показателя надежности.

Относительная ошибка переноса опытных значений показателя надежности на генеральную совокупность:

(1.35)

Определяем доверительные границы рассеивания одиночного и среднего значений показателя надежности, предварительно задаемся доверительной вероятностью α = 0,95. По таблице определяем значение коэффициента Стьюдента для α = 0,95 и N = 30. Для заданных условий = 2,04. Тогда, по формулам 1.27, 1.28, 1.30 и 1.31 определим:

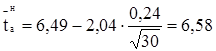мм;

мм;

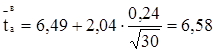мм;

мм;

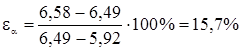
Расчет доверительных границ рассеивания при использовании закона распределения Вейбулла ведется от нуля, т.к. кривая распределения в этом случае асимметрична.

Рассеивание одиночных значений показателя надежности определяется по формулам:

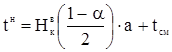, (1.36)

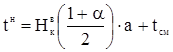(1.37)

где tн – нижняя доверительная граница;