Курсовая работа: Плоский рычажной механизма

Чтобы условие соосности выполнялось в любом случае, умножим правую часть равенства на левую, а левую - на правую:

(a + b) * (d - с) = (d - с) * (a + b).

Так как сомножители a, b, c, d пропорциональны числам зубьев, то для определения последних требуется умножить каждый сомножителей на коэффициент пропорциональности γ. Очевидно, что γ - любое положительное число. Таким образом, получим:

γ * (a + b) * (d - с) = γ * (d - с) * (a + b).

Преобразуем равенство к виду:

γ * a * (d - с) + γ * b * (d - с) = γ * d * (a + b) - γ * с * (a + b).

Теперь можно принять, что:

Z₁ = γ * a * (d - с), Z₂ = γ * b * (d - с),

Z₃ = γ * с * (a + b), Z₄ = γ * d * (a + b).

Разобьём передаточное отношение на четыре сомножителя, которые должны быть целыми числами. Это можно выполнить различным образом:

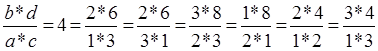
Рассмотрим третий вариант: а = 2, b = 3, с = 3, d = 8. Решение ищем в ранее полученном виде:

Z₁ = γ * a * (d - с) = 2 * (8 - 3) * γ = 2 * γ,

Z₂ = γ * b * (d - с) = 3 * (8 - 3) * γ = 3 * γ,

Z₃ = γ * с * (a + b) = 3 * (2 + 3) * γ = 3 * γ,

Z₄ = γ * d * (a + b) = 8 * (2 + 3) * γ = 8 * γ.

Наименьшим должно быть зубчатое колесо Z₁ . Число зубьев колеса Z₁ определяется из условия отсутствия интерференции зубьев при зацеплении с колесом Z₂ ; Z₁ должно быть более 17, так как при 17 зубьях правильное зацепление возможно лишь с зубчатой рейкой. Примем γ = 9, тогда:

Z₁ = 18, Z₂ = 27, Z₃ = 27, Z₄ = 72.

Условия правильного зацепления выполняется (согласно таблице):

Z₁ > 17, а Z₄ > Z₃ + 8.

Определим возможное число сателлитов по внешнему зацеплению:

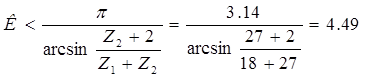
По внутреннему зацеплению:

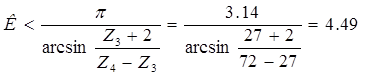
Число сателлитов может быть не более трёх. Проверим условие сборки при трёх сателлитах:

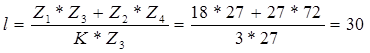
Условие сборки выполняется, так как l = 30 - целое число.

Определяем диаметры делительных окружностей зубчатых колёс:

d₁ = Z₁ * m = 18 * 4 = 72 мм,