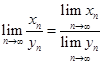Курсовая работа: Предел последовательности. Теорема Штольца

Теорема 4:

Если последовательности {x_n } и {у_n } сходятся, то и последовательность {x_n * у_n } также сходится и её предел равен произведению её множителей (пределов).

Доказательство:

x_n → a, следовательно x_n = a + α_n

у_n → b, следовательно у_n = b + β_n

x_n * у_n = (а + α_n )*(b + β_{n )} =аb+(а β_n + bα_n + α_n β_n )

обозначим γ_n = а β_n + bα_n + α_n β_n , где γ_n элемент бесконечно малой последовательности, получается

x_n * у_n = ab+ γ_{n ,}

следовательно,

Теорема 5:

Если последовательности {x_n } и {у_n } сходятся к числам а и b соответственно, и если b ≠ 0, предел частного существует, конечен и равен частному пределов.

Доказательство:

Т.к. последовательность {у_n } сходится к b, то по определению сходящейся последовательности, для любого ε > 0, найдётся N(ε), такой что для всех n > N, будет выполнятся неравенство |b– y_n |< ε.

Тогда положив , видим, что

,

откуда следует

следовательно

.

Т.к., согласно условию b ≠ 0, то из последнего неравенства следует, что для всех n > N элементы последовательности {у_n } не равны 0, значит именно с этого номера N можно определить последовательность

x_n = a + α_n

у_n = b + β_{n ,} следовательно

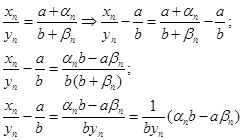
обозначим γ_n = α_п b – aβ_n , γ_n элемент бесконечно малой последовательности.

,

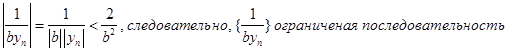а тогда из последнего равенства, следует

, откуда