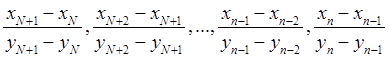Курсовая работа: Предел последовательности. Теорема Штольца
Числовая последовательность задана общим членом xп, рассмотрим его:
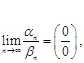
при нахождении такого предела говорят, что будем раскрывать неопределённость вида 
.
при нахождении такого предела, говорят, что будем раскрывать неопределенность вида 
.
Для раскрытия неопределённости доделим числитель и знаменатель на наибольшую степень n.
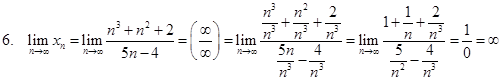
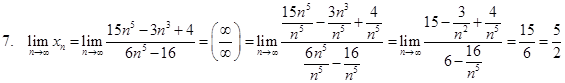
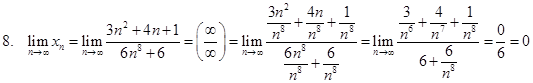
Таким образом, имеет место правило:
Предел отношения двух многочленов равен бесконечности, если степень числителя больше степени знаменателя, нулю, если степень числителя меньше степени знаменателя и отношению коэффициентов при старших членах, если степени числителя и знаменателя равны.
Для упрощения задачи нахождения предела последовательности, вышеуказанного вида, мы прибегаем к помощи теоремы Штольца.
Теорема Штольца
Для определения пределов неопределённых выражений 
типа 
часто бывает полезна следующая теорема, принадлежащая Штольцу (O. Stolz).
Теорема: Пусть варианта 
, причём – хотя бы начиная с некоторого места – с возрастанием п и уп возрастает: т.е. уп+1 > yn . Тогда
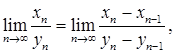
если только существует предел справа (конечный или даже бесконечный).
Доказательство: Допустим сначала, что этот предел равен конечному числу L:
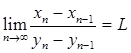
Тогда по любому заданному 
найдется такой номер N, что для n > N будет
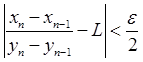
или
.
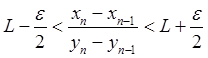Значит, какое бы n > N ни взять, все дроби
