Курсовая работа: Разработка следящей системы промышленного робота

Очевидно, что требования по статической ошибке мы выполнили. В свою очередь общий коэффициент усиления - К определяется произведением:

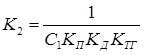
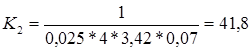
Таким образом, мы получили К такое, что удовлетворяются условия заданной точности и полностью решили требуемую задачу, т.е.

Передаточная функция сервопривода примет следующий вид:

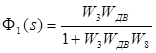
, где сервопривод безкоррекции.

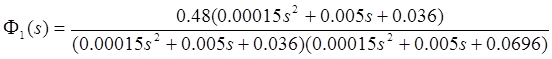
Проверяем на устойчивость по алгебраическому критерию – критерию Гурвица. Строим матрицу Гурвица

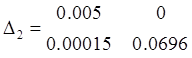
для того чтобы система была устойчива необходимо и достаточно, чтобы все главные миноры (диагональ) матрицы Гурвица были положительны (>0) определители больше нуля следовательно система устойчива. Строим переходный процесс в сервоприводе

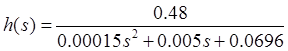
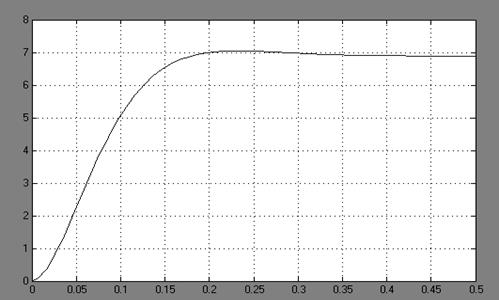
Рисунок 3.1 - Переходный процесс в сервоприводе и по нему определяем прямые показатели качества:

- время регулирования t_P = 0.15c

- перерегулирование σ =2,9%

Решение задачи обеспечения прямых показателей качества

При невозможности решить задачу повышения запасов устойчивости в рамках имеющейся системы приходится идти на изменение структуры, т.е. вводят корректирующие звенья в систему. Для решения этой задачи будем использовать метод академика Солодовникова. С помощью этого метода мы синтезируем новое звено в сервоприводе. При этом структура корректирующего звена неизвестна, необходимо с помощью метода ЛАЧХ Солодовникова выбрать звено таким образом, чтобы прямые показатели качества были бы не хуже заданным по ВЗ.

Структурная схема САУ сводится к виду

Такое приведение схемы может быть сделано, так как передаточная функция обратной связи W₈ является безинерционным звеном. Обозначим произведение передаточных функций прямой цепи, как передаточную функцию неизменяемой части системы :

Структурную схему можно представить в следующем виде:

Рисунок 3.3 - Структурная схема САУ