Курсовая работа: Решение обратной задачи динамики
В прикладных задачах параметрической оптимизации не всегда используются интегральные квадратичные оценки, порядок которых равен порядку дифференциального уравнения оптимизируемой системы. Очень часто параметрический синтез проводят по квадратичным оценкам первого и второго порядка. В таких случаях параметры системы определяются из условия, чтобы выходная переменная x (t ) приближалась к решению дифференциального уравнения первого или соответственно второго порядка.
Таким образом, требование оптимальности системы по переходному процессу в смысле минимума интегральной квадратичной оценки ![]() равносильно требованию, чтобы выходная переменная системы в ее свободном движении изменялась в соответствии с решением однородного дифференциального уравнения порядка m .
равносильно требованию, чтобы выходная переменная системы в ее свободном движении изменялась в соответствии с решением однородного дифференциального уравнения порядка m .
В последнее время при анализе и синтезе систем автоматического управления широкое применение нашли спектральные методы, которые базируются на спектральных характеристиках сигналов, что значительно упрощает решение задач теории управления с использованием ЭВМ. Ниже рассмотрим теоретические основы применения спектральных методов при решении задач теории управления.
Применение спектрального метода для решения обратных задач динами
Рассмотрим решение спектральным методом обратной задачи динамики в следующей постановке.
Известна система автоматического управления (регулирования), которая может быть как стационарной, так и нестационарной, и работа которой описывается следующим дифференциальным уравнением:
![]() (2.1)
(2.1)
где
![]() - сигнал на выходе системы;
- сигнал на выходе системы;
![]() - сигнал на входе системы;
- сигнал на входе системы;
![]() - коэффициенты дифференциального уравнения, являющиеся функциями времени.
- коэффициенты дифференциального уравнения, являющиеся функциями времени.
При этом неизвестны некоторые параметры настройки системы управления, которые необходимо определить в процессе решения задачи. Обозначим множество этих параметров через ![]() где
где ![]() - их число. Тогда коэффициенты дифференциального уравнения будут зависеть от
- их число. Тогда коэффициенты дифференциального уравнения будут зависеть от ![]() и, следовательно можно записать;
и, следовательно можно записать;
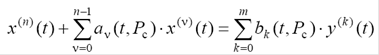 (2.2)
(2.2)
Задан эталонный сигнал ![]() на интервале
на интервале ![]() или его спектральная характеристика, который необходимо получить на выходе системы (2.2). В общем случае могут быть заданы ненулевые начальные условия:
или его спектральная характеристика, который необходимо получить на выходе системы (2.2). В общем случае могут быть заданы ненулевые начальные условия:
![]() (2.3)
(2.3)
Для заданных дифференциального уравнения (2.2), эталонного выходного сигнала ![]() и начальных условий (2.3) необходимо определить входной сигнал
и начальных условий (2.3) необходимо определить входной сигнал ![]() и искомые сигнала на выходе получили бы сигнал, максимально параметры настройки
и искомые сигнала на выходе получили бы сигнал, максимально параметры настройки ![]() такими, что при подачи на вход системы автоматического управления найденного входного в известном смысле приближенный к эталонному.
такими, что при подачи на вход системы автоматического управления найденного входного в известном смысле приближенный к эталонному.
В качестве меры близости реального сигнала на выходе системы (2.2), (2.3) к эталонному сигналу ![]() на интервале
на интервале ![]() примем следующий функционал
примем следующий функционал
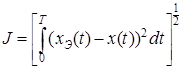 (2.4)
(2.4)
Неизвестный входной сигнал будем искать в форме его спектрального разложения в ряд по некоторому базису ортонормированных функций ![]() ;
;
![]()
где коэффициенты ![]() , неизвестны и их необходимо определить.
, неизвестны и их необходимо определить.
Следовательно входной сигнал будет зависеть от времени ![]() и от множества параметров
и от множества параметров ![]() Тогда дифференциальное уравнение (2.2) можно записать в следующей виде
Тогда дифференциальное уравнение (2.2) можно записать в следующей виде
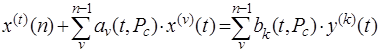 (2.5)
(2.5)
Интегрируя уравнение ![]() раз с учетом начальных условий, получим
раз с учетом начальных условий, получим
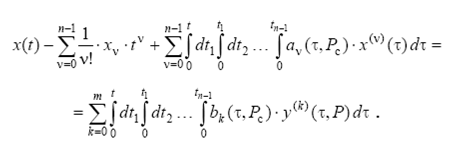 (2.6)
(2.6)
Воспользовавшись справедливым для любой непрерывной функции тождеством
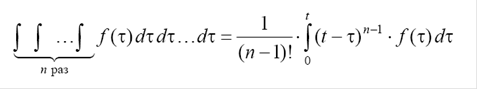
равенство (2.6) можно переписать в виде
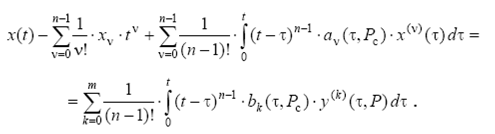 (2.7)
(2.7)