Курсовая работа: Решение обратной задачи динамики

, (2.13)

где - спектральная характеристика сигнала на входе системы, элементы которой определяются из соотношения

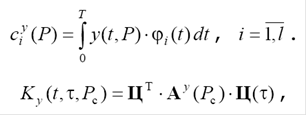(2.14)

где - квадратная матрица размерностью спектральной характеристики форсирующей части системы, элементы которой определяются из выражения

(2.15)

где - матрица размерностью элементы которой определяются из соотношения

Подставляя разложения (2.13), (2.14) и (2.15) в (2.9) и делая соответствующие преобразования, получим

(2.16)

Таким образом, уравнение (2.9) с учетом (2.12) и (2.16) можно переписать в следующем виде

(2.17)

Рассмотрим теперь функционал (2.4). Имеем

Так как , то последние выражение можно записать в следующем виде

(2.18)

или

где

. (2.19)

Здесь спектральная характеристика эталонного сигнала или задана или, в случае задании эталонного сигнала , определяется из выражения

, .

Таким образом, задача определения входного сигнала (точнее множества ) и множества неизвестных параметров настройки системы управления (2.2), (2.3) сводиться к задаче безусловной минимизации функционала (2.18) по элементам множеств и , т.е.

.

Практическая часть

Результаты расчётов:

1. Интервал исследования

tmin = 0.000000e+000, c;