Курсовая работа: Решения задач линейного программирования геометрическим методом

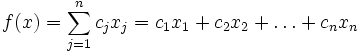
Нужно максимизировать

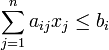
при условиях при i= 0, 1, 2, . . . , m .

Иногда на x_i также накладывается некоторый набор ограничений в виде равенств, но от них можно избавиться, последовательно выражая одну переменную через другие и подставляя ее во всех остальных равенствах и неравенствах (а также в функции f).

Такую задачу называют "основной" или "стандартной" в линейном программировании.

1.2 Формулировка задачи

Даны линейная функция Z=С₁ х₁ +С₂ х₂ +...+С_N x_N (1.1)

и система линейных ограничений

a₁₁ x₁ + a₂₂ x₂ + ... + a_1N Х_N = b₁

a₂₁ x₁ + a₂₂ x₂ + ... + a_2N Х_N = b₂

. . . . . . . . . . . . . . .

a_i1 x₁ + a_i2 x₂ + ... + a_iN Х_N = b_i (1.2) . . . . . . . . . . . . . . .

a_M1 x₁ + a_M2 x₂ + ... + a_MN Х_N = b_M

x_j 0 (j = 1, 2, ... ,n) (1.3)

где а_ij , b_j и С_j - заданные постоянные величины.

Найти такие неотрицательные значения х₁ , х₂ , ..., х_n , которые удовлетворяют системе ограничений (1.2) и доставляют линейной функции (1.1) минимальное значение.

Общая задача имеет несколько форм записи.

Векторная форма записи. Минимизировать линейную функцию Z = СХ при ограничениях А₁ х₁ + А₂ x₂ + ... + А_N x_N = А_о , X₀ (1.4)

где С = (с₁ , с₂ , ..., с_N ); Х = (х₁ , х₂ , ..., х_N ); СХ - скалярное произведение; векторы A₁ = A₂ = ,..., A_N состоят соответственно из коэффициентов при неизвестных и свободных членах.

Матричная форма записи . Минимизировать линейную функцию, Z = СХ при ограничениях АХ = А₀ Х₀ , где С = (с₁ , с₂ , ..., с_N ) - матрица-cтрока; А = (а_ij ) - матрица системы; Х =(x_ij )- матрица-столбец, А₀ = (а_i ) матрица-столбец

Запись с помощью знаков суммирования. Минимизировать линейную функцию Z = С_j х_j при ограничениях

0пределение 1. Планом или допустимым решением задачи линейного программирования называется Х = (х₁ , х₂ , ..., х_N ), удовлетворяющий условиям (1.2) и (1.3).

0пределение 2. План Х = (х₁ , х₂ , ..., х_N ) называется опорным, если векторы А (i = 1, 2, ..., N), входящие в разложение (1.4) с положительными коэффициентами х , являются линейно независимыми.

Так как векторы А являются N-мерными, то из определения опорного плана следует, что число его положительных компонент не может превышать М.

0пределение 3. Опорный план называется невырожденным, если он содержит М положительных компонент, в противном случае опорный план называется вырожденным.

0пределение 4. Оптимальным планом или оптимальным решением задачи линейного программирования называется план, доставляющий наименьшее (наибольшее) значение линейной функции.

В дальнейшем рассмотрено решение задач линейного программирования, связанных с нахождением минимального значения линейной функции. Там, где необходимо найти максимальное значение линейной функции, достаточно заменить на противоположный знак линейной функции и найти минимальное значение последней функции. Заменяя на противоположный знак полученного минимального значения, определяем максимальное значение исходной линейной функции.

1.3 Основные понятия линейной алгебры и выпуклого анализа, применяемые в теории математического программирования

Кратко напомним некоторые фундаментальные определения и теоремы линейной алгебры и выпуклого анализа, которые широко применяются при решении проблем как линейного, так и нелинейного программирования.

Фундаментальным понятием линейной алгебры является линейное (вещественное) пространство. Под ним подразумевается множество некоторых элементов (именуемых векторами или точками), для которых заданы операции сложения и умножения на вещественное число (скаляр), причем элементы, являющиеся результатом выполнения операций, также в соответствии с определением должны принадлежать исходному пространству.