Курсовая работа: Решения задач линейного программирования геометрическим методом

а₂₁ х₁ + а₂₂ х₂ + … + а_{2 n} х _n ≤ b ₂

……………………………..

(***)

а _{m 1} х₁ + а _{m 2} х₂ + … + а _mn х _n ≤ b_m

х _j ≥ 0, j = 1, 2, …, n .

Рассмотрим эту задачу на плоскости, т.е. при п = 2. Пусть система неравенств (**), (***) совместна (имеет хотя бы одно решение):

а₁₁ х₁ + а₁₂ х₂ ≤ b ₁

а₂₁ х₁ + а₂₂ х₂ ≤ b ₂

…………..

а _{m 1} х₁ + а _{m 2} х₂ ≤ b_m

x ₁ ≥ 0; х₂ ≥ 0.

Каждое неравенство этой системы геометрически определяет полуплоскость с граничной прямой а _{i 1} х₁ + а _{i 2} х₂ ≤ b_i i = 1, m . Условия неотрицательности определяют полуплоскости соответственно с граничными прямыми x ₁ = 0; х₂ = 0. . Система совместна, поэтому полуплоскости, как выпуклые множества, пересекаясь, образуют общую часть, которая является выпуклым множеством и представляет собой совокупность точек, координаты каждой из которых составляют решение данной системы. Совокупность этих точек называют многоугольником решений. Это может быть точка, отрезок, луч, замкнутый многоугольник, неограниченная многоугольная область.

Если в системе ограничений (**) - (***) n = 3, то каждое неравенство геометрически представляет полупространство трехмерного пространства, граничная плоскость которого а _{i 1} х₁ + а _{i 2} х₂ + а _{i 3} х₁ ≤ b_i , а условия неотрицательности — полупространства с граничными плоскостями соответственно x_i = 0 ( i = 1, 2, 3) . Если система ограничений совместна, то эти полупространства, как выпуклые множества, пересекаясь, образуют в трехмерном пространстве общую часть, которая называется многогранником решений.

Пусть в системе (**) - (***) п > 3, тогда каждое неравенство определяет полупространство n-мерного пространства с граничной гиперплоскостью а _{i 1} х₁ + а _{i 2} х₂ + … + а _in х _n ≤ b_i i = 1, т , а условия неотрицательности — полупространства с граничными гиперплоскостями x_j = 0, j = 1, n .

Если система ограничений совместна, то по аналогии с трехмерным пространством она образует общую часть n-мерного пространства, называемую многогранником решений, так как координаты каждой его точки являются решением.

Таким образом, геометрически задача линейного программирования представляет собой отыскание такой точки многогранника решений, координаты которой доставляют линейной функции минимальное значение, причем допустимыми решениями служат все точки многогранника решений.

1.4.3 Этапы решения графического метода задач линейного программирования

Графический метод основан на геометрической интерпретации задачи линейного программирования и применяется в основном при решении задач двумерного пространства и только некоторых задач трехмерного пространства, так как довольно трудно построить многогранник решений, который образуется в результате пересечения полупространств. Задачу пространства размерности больше трех изобразить графически вообще невозможно.

Пусть задача линейного программирования задана в двумерном пространстве, т. е. ограничения содержат две переменные.

Если в ЗЛП ограничения заданы в виде неравенств с двумя переменными, она может быть решена графически. Графический метод решения ЗЛП состоит из следующих этапов.

Этап 1.

Сначала на координатной плоскости x ₁ Ox ₂ строится допустимая многоугольная область (область допустимых решений, область определения), соответствующая ограничениям:

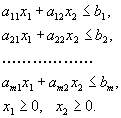1.6)

Не приводя строгих доказательств, укажем те случаи, которые тут могут получится.

1. Основной случай - получающаяся область имеет вид ограниченного выпуклого многоугольника (рис. 1а).

2. Неосновной случай  получается неограниченный выпуклый многоугольник, имеющий вид, подобный изображенному на рис. 1б. Подобная ситуация, например, получится, если в рассмотренном выше примере убрать ограничение х₁ + х ₂ ≤ 3. Оставшаяся часть будет неограниченным выпуклым многоугольником.

Рис. 1

б)

а)

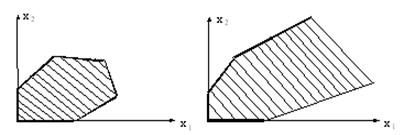
Наконец, возможен случай, когда неравенства (1.6) противоречат друг другу , и допустимая область вообще пуста .

Рассмотрим теорию на конкретном примере:

Найти допустимую область задачи линейного программирования, определяемую ограничениями

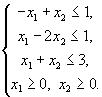1.32)

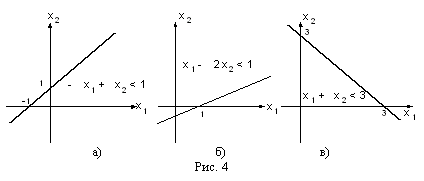
Решение: