Курсовая работа: Решения задач линейного программирования геометрическим методом

Чтобы учесть оставшиеся ограничения, проще всего заменить неравенства на равенства, в результате чего получится система уравнений прямых:

3х₁ + х₂ = 75;

х₁ + х₂ = 30;

х₁ +4х₂ = 84.

а затем на плоскости провести эти прямые.

Например, неравенство 3х₁ + х₂ ≤ 75 заменяется уравнением прямой 3х₁ + х₂ = 75. Чтобы провести эту линию, надо найти две различные точки, лежащие на этой прямой Можно положить х₁ = 0, тогда х₂ = 75/1 = 75.. Аналогично для х₂ = 0 находим x₁ = 75/3 = 25. Итак, наша прямая проходит через две точки (0, 75) и (25;0). Аналогично найдём остальные точки и запишем их в таблицу 1.2..

Таблица 1.2.

3х1 +х2 ≤ 75;		х1 +х2 ≤ 30;		х1 +4х2 ≤ 84.
х1	х2	х1	х2	х1	х2
0	75	0	30	0	21
25	0	30	0	84	0

Согласно данной таблицы, построим график в программе Excel.

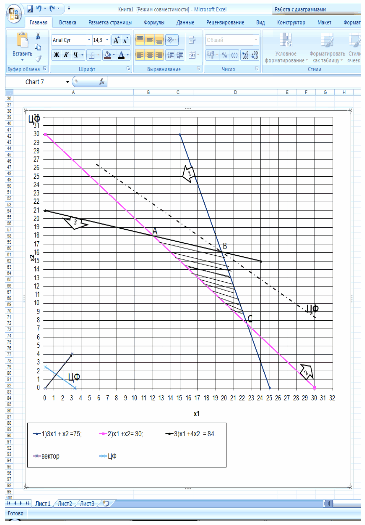
Заштрихованная область, изображённая на рисунке, является областью допустимых значений функции F. Т.к. целевая функция F стремиться к max, то идя по направлению вектора n, получим точку B с оптимальным решением. Для определения ее координаты возьмем две прямые, на пересечении которых она образуется:

3х₁ + х₂ ≤ 75, х₁ = 19,64,

х₁ + 4х₂ ≤ 84, х₂ = 16,09. , т. е. B(16,09; 19,64)

максимальное значение линейной функции равно :

F_max = 30*16,09 + 40*19,64 = 1232,80.

Итак, F_max = 1232,80 при оптимальном решении х₁ = 16,09, х₂ = 19,64, т. е. максимальная прибыль в 1232,80 ден. ед. может быть достигнута при производстве 16,09 единиц продукции А и 19,64 единиц продукции В.

Ответ: F_max = 1232,80.

Задача № 2

Для изготовления двух видов продукции Р₁ и Р₂ используют три вида сырья: S₁ , S₂ , S₃ . Запасы сырья, количество единиц сырья, затрачиваемых на изготовление единицы продукции, а также величина прибыли, получаемая от реализации единицы продукции, приведены в таблице 2.1.

Таблица 2.1.

Вид сырья	Запас сырья	Количество единиц сырья, идущих на изготовление единицы продукции
		Р1	Р2
S1	20	2	5
S2	40	8	5
S3	30	5	6
Прибыль от единицы продукции, руб.		50	40

Необходимо составить такой план выпуска продукции, чтобы при ее реализации получить максимальную прибыль.

Решение.

Обозначим через х₁ количество единиц продукции Р₁ , а через х₂ – количество единиц продукции Р₂ . Тогда, учитывая количество единиц сырья, расходуемое на изготовление продукции, а так же запасы сырья, получим систему ограничений:

2х₁ + 5х₂ ≤ 20

8х₁ + 5х₂ ≤ 40

5х₁ + 6х₂ ≤ 30

которая показывает, что количество сырья, расходуемое на изготовление продукции, не может превысит имеющихся запасов. Если продукция Р₁ не выпускается, то х₁ =0; в противном случае x₁ = 0. То же самое получаем и для продукции Р₂ . Таким образом, на неизвестные х₁ и х₂ должно быть наложено ограничение неотрицательности: х₁ ≥ 0, х₂ ≥ 0.

Конечную цель решаемой задачи – получение максимальной прибыли при реализации продукции – выразим как функцию двух переменных х₁ и х₂ . Реализация х₁ единиц продукции Р₁ и х₂ единиц продукции Р₂ дает соответственно 50х₁ и 40х₂ руб. прибыли, суммарная прибыль Z = 50х₁ + 40х₂ (руб.)

Условиями не оговорена неделимость единица продукции, поэтому х₁ и х₂ (план выпуска продукции) могут быть и дробными числами.

Требуется найти такие х₁ и х₂ , при которых функция Z достинает максимум, т.е. найти максимальное значение линейной функции Z = 50х₁ + 40х₂ при ограничениях

2х₁ + 5х₂ ≤ 20