Курсовая работа: Решения задач линейного программирования геометрическим методом

2. Рассмотрим прямую . При , а при . Таким образом, эта прямая проходит через точки (0, -1/2) и (1,0). так как (4.б).

3. Наконец, рассмотрим прямую . Она проходит через точки (0,3) и (3,0) и так как 0+0<3, то интересующая нас полуплоскость лежит ниже прямой, изображенной на рис. 4.в.

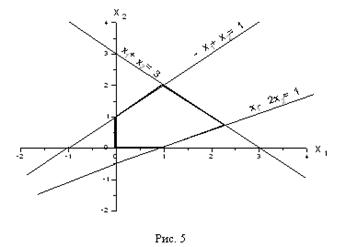
Сводя все вместе и добавляя условия х₁ ≥ 0,х₂ ≥ 0 получим рисунок 5, где выделена область, в которой выполняются одновременно все ограничения (1.32). Обратим внимание на то, что получившаяся область имеет вид выпуклого многоугольника .

Этап 2.

Вернёмся теперь к исходной задаче линейного программирования. В ней, кроме системы неравенств, есть еще целевая функция с₁ х₁ +с₂ х₂ =>max.

Рис. 6

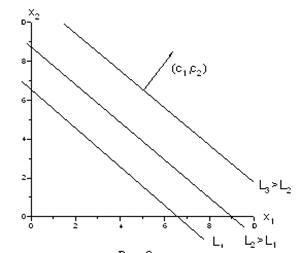
Рассмотрим прямую с₁ х₁ +с₂ х₂ = L. Будем увеличивать L. Что будет происходить с нашей прямой?

Легко догадаться, что прямая будет двигаться параллельно самой себе в том направлении, которое дается вектором (с₁ ,с₂ ), так как это  вектор нормали к нашей прямой и одновременно вектор градиента функции

f(х₁ ,х₂ ) = с₁ х₁ +с₂ х₂ .

А теперь сведем всё вместе. Итак, надо решить задачу

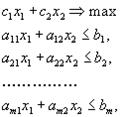
Ограничения задачи вырезают на плоскости некоторый многоугольник. Пусть при некотором L прямая с₁ х₁ +с₂ х₂ = Lпересекает допустимую область. Это пересечение дает какие-то значения переменных (х₁ ,х₂ ), которые являются планами.

Этап 3

Увеличивая L мы начнем двигать нашу прямую и её пересечение с допустимой областью будет изменяться (см. рис. 7). В конце концов эта прямая выйдет на границу допустимой области  как правило, это будет одна из вершин многоугольника . Дальнейшее увеличение L приведёт к тому, что пересечение прямой с₁ х₁ +с₂ х₂ = Lс допустимой областью будет пустым. Поэтому то положение прямой с₁ х₁ +с₂ х₂ = L, при котором она вышла на граничную точку допустимой области, и даст решение задачи, а соответствующее значение L и будет оптимальным значением целевой функции.

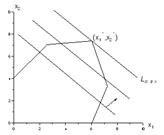???. 7

II . ПРАКТИЧЕСКИЙ РАЗДЕЛ

Задача №1

Для производства двух видов изделий А и В предприятие использует три вида сырья. Другие условия задачи приведены в таблице 1.1..

Таблица 1.1.

Вид сырья	Нормы расхода сырья на одно изделие, кг AB	Общее количество сырья, кг
I	12 4	300
II	4 4	120
III	3 12	252
Прибыль от реализации одного изделия, ден. ед.	30 40	?

Составить такой план выпуска продукции, при котором прибыль предприятия от реализации продукции будет максимальной при условии, что изделие В надо выпустить не менее, чем изделия А.

Решение.

Обозначим через х₁ и х₂ количество единиц продукции соответственно А и В, запланированных к производству. Для их изготовления потребуется (12 х₁ +4х₂ ) единиц ресурса I, (4х₁ +4х₂ ) единиц ресурса II, (3х₁ +12х₂ ) единиц ресурса III. Так как, потребление ресурсов I, II, III не должно превышать их запасов, то связь между потреблением ресурсов и их запасами выразится системой неравенств:

12х₁ +4х₂ ≤ 300; 3х₁ + х₂ ≤ 75;

4х₁ +4х₂ ≤ 120; х₁ + х₂ ≤ 30;

3х₁ +12х₂ ≤ 252. х₁ +4х₂ ≤ 84.

По смыслу задачи переменные х₁ ≥ 0, х₂ ≥0. (1,1)

Конечную цель решаемой задачи – получение максимальной прибыли при реализации продукции – выразим как функцию двух переменных х₁ и х₂ .

Суммарная прибыль А составит 30х₁ от реализации продукции А и 40х ₂ от реализации продукции В, то есть : F = 30х₁ +40х _2. (1,2)

Изобразим многоугольник решений данной задачи.

В ограничениях задачи поменяем знаки неравенства на знаки равенства.