Курсовая работа: Решения задач линейного программирования геометрическим методом
Вектор λ1 a1 + λ2 a2 + …+ λm am называется линейной комбинацией векторов а1 а2 ,..., аm с коэффициентами λ1 , λ2, λm ,
Система векторов линейного пространства а1 а2 ,..., аm называется линейно зависимой, если существуют такие числа λ1 , λ2, λm не равные одновременно нулю, что их линейная комбинация λ1 a1 + λ2 a2 + …+ λm am равняется нулевому вектору (вектору, все компоненты которого равны нулю). В противном случае систему а1 , а2 ,..., аm называют линейно независимой, т. е. линейная комбинация данных векторов может быть равна нулевому вектору только при нулевых коэффициентах λ1 , λ2, …, λm
Максимально возможное количество векторов, которые могут образовывать линейно независимую систему в данном линейном пространстве, называют размерностью пространства, а любую систему линейно независимых векторов в количестве, равном размерности, — базисом пространства.
Линейное пространство обычно обозначают как Rn , где n — его размерность.
Любое подмножество данного линейного пространства, которое само обладает свойствами линейного пространства, называется линейным подпространством. Множество Н, получаемое сдвигом некоторого линейного подпространства L€ Rn на вектор a€ Rn : H=L+a, называется аффинным множеством (пространством). Если фундаментальным свойством любого линейного пространства или подпространства является принадлежность ему нулевого вектора, то для аффинного множества это не всегда так. На плоскости примером подпространства является прямая, проходящая через начало координат, а аффинного множества — любая прямая на плоскости. Характеристическим свойством аффинного множества является принадлежность ему любой прямой, соединяющей две любые его точки. Размерность аффинного множества совпадает с размерностью того линейного подпространства, сдвигом которого оно получено.
Если рассматривается некоторое линейное пространство Rn , то принадлежащие ему аффинные множества размерности 1 называются прямыми, а размерности (n-1)—гиперплоскостями. Так, обычная плоскость является гиперплоскостью для трехмерного геометрического пространства R3 , а прямая — гиперплоскостью для плоскости R2 . Всякая гиперплоскость делит линейное пространство на два полупространства.
Множество V векторов (точек) линейного пространства Rn называется выпуклым, если оно содержит отрезок прямой, соединяющей две его любые точки, или, другими словами, из того, что a€V и b€V , следует, что х = (1- λ) х а+ λ х b€ V , где 0 ≤ λ≤ 1.
Линейная комбинация ![]() векторов а1 , а2 ... аm называется выпуклой, если λi ≥0, i€1:m и
векторов а1 , а2 ... аm называется выпуклой, если λi ≥0, i€1:m и ![]()
Множество, содержащее все возможные выпуклые комбинации точек некоторого множества М, называют выпуклой оболочкой данного множества. Можно показать, что выпуклая оболочка множества М является наименьшим выпуклым множеством, содержащим М.
Выпуклая оболочка конечного множества точек называется выпуклым многогранником, а непустое пересечение конечного числа замкнутых полупространств — многогранным выпуклым множеством. В отличие от выпуклого многогранника последнее может быть неограниченным.
Точка v выпуклого множества V называется его угловой (крайней) точкой, если она не является внутренней точкой ни для какого отрезка, концы которого принадлежат множеству V. Угловые точки выпуклого многогранника являются его вершинами, а сам он — выпуклой оболочкой своих вершин.
Множество К называется конусом с вершиной в точке x0 , если x0 € К , и из того, что некоторая точка х принадлежит К ( х € К ), следует, что в К содержится и луч, начинающийся в х0 и проходящий через х, т. е.
![]()
или
![]()
Выпуклая оболочка конечного множества лучей, исходящих из одной точки, называется многогранным выпуклым конусом с вершиной в данной точке.
1.4 Математические основы решения задачи линейного программирования графическим способом
1.4.1 Математический аппарат
Для понимания всего дальнейшего полезно знать и представлять себе геометрическую интерпретацию задач линейного программирования, которую можно дать для случаев n = 2 и n = 3.
Наиболее наглядна эта интерпретация для случая n = 2, т.е. для случая двух переменных x1 и x2 . Пусть нам задана задача линейного программирования в стандартной форме
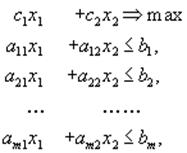 1.5)
1.5)
![]()
Возьмём на плоскости декартову систему координат и каждой паре чисел (x1 ,x2 )поставим в соответствие точку на этой плоскости.
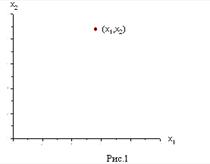
Обратим прежде всего внимание на ограничения x1 ≥0 и x2 ≥ 0. Они из всей плоскости вырезают лишь её первую четверть (см. рис. 1). Рассмотрим теперь, какие области соответствуют неравенствам вида a1 x1 + a2 x2 ≤ b. Сначала рассмотрим область, соответствующую равенству a1 x1 + a2 x2 = b. Как Вы, конечно, знаете, это прямая линия. Строить её проще всего по двум точкам.
Пусть b ≠ 0. Если взять x1 = 0, то получится x2 = b/a2 . Если взять x2 = 0, то получится x1 = b/a1 . Таким образом, на прямой лежат две точки (0, b/a2 ) и (b/a1 , 0). Дальше через эти две точки можно по линейке провести прямую линию (рисунок 2).
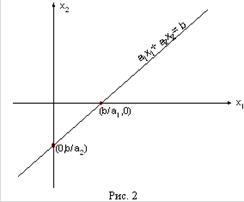
Если же b=0, то на прямой лежит точка (0,0). Чтобы найти другую точку, можно взять любое отличное от нуля значениеx1 и вычислить соответствующее ему значение x2 .
Эта построенная прямая разбивает всю плоскость на две полуплоскости. В одной её части a1 x1 + a2 x2 < b, а в другой наоборот a1 x1 + a2 x2 > b. Узнать, в какой полуплоскости, какой знак имеет место проще всего посмотрев, какому неравенству удовлетворяет какая-то точка плоскости, например, начало координат, т.е. точка (0,0).
1.4.2 Геометрическая интерпретация задачи линейного программирования
Рассмотрим задачу ЛП в стандартной форме записи:
max f ( X ) = с1 х1 + с2 х2 + ... + сп хп (*)