рисунок 1.10 - функциональная схема системы подчиненного управления

1.6 Исследование переходных процессов в системе подчиненного управления

Исследование переходных процессов в данной системе произведем с помощью программы «Matlab». Моделирование системы произведем для ее расчетных параметров и для случаев увеличения и уменьшения Т_М и Т_Э в два раза. Математическая модель системы подчиненного управления представлена на рисунке 1.11

Рисунок 1.12 – Переходные процессы при расчетных параметрах

Рисунок 1.13 – Переходные процессы при уменьшении Т_Я в 2 раза

Рисунок 1.14 – Переходные процессы при увеличении Т_Я в 2 раза

Рисунок 1.15 – Переходные процессы при уменьшении Т_М в 2 раза

Рисунок 1.16 – Переходные процессы при увеличении Т_М в 2 раза

Моделирование показало, что уменьшение Тя уменьшает колебательность и перерегулирование в системе. Увеличение Т_Я существенно увеличивает колебательность и перерегулирование в системе. При уменьшении Т_М в системе увеличивается перерегулирование, но установившееся значение тока двигателя уменьшается. Увеличение Т_М в 2 раза приводит к увеличению тока двигателя и времени разгона, но в свою очередь значительно уменьшает перерегулирование.

2. Синтез релейной системы

При разработке системы управления электроприводом определенного класса механизмов возможно успешное применение аналитического конструирования регуляторов, с помощью которого синтезируются структурные схемы управления, обеспечивающие движение электропривода с выполнением заданного критерия качества.

Наиболее перспективным для решения задач синтеза систем оптимального управления является метод динамического программирования Р. Беллмана. Применение этого метода с использованием в качестве критерия оптимальности минимума интегральной ошибки позволяет получить алгоритм оптимального управления регулятора, не только оптимизируя принятый функционал качества, но и обеспечивающий устойчивость движения фазовых координат объекта управления.

Если силовые части объекта управления описываются линейными дифференциальными уравнениями и в качестве критерия оптимальности принимается минимум интегральной квадратичной ошибки, с помощью указанной методики можно получить алгоритмы оптимальных управлений в функции фазовых координат. Это обеспечивает легкую реализацию такой системы управления, так как все обратные связи оказываются жесткими. Однако статическая ошибка в такой системе, возникающая при наличии статического момента на валу, не равна нулю и по своей величине близка к ошибке однократно интегрирующей линейной системы. В связи с этим актуальным является создание системы с гибкой обратной связью по одной лишь выходной координате. Статизм такой системы равен нулю, что соответствует требованиям.

Применение в качестве регуляторов фазовых координат релейных элементов, работающих в скользящем режиме, позволяет без потерь устойчивости получить очень большие коэффициенты усиления. Тем самым обеспечивается не только оптимизация управления, но инвариантность системы к параметрическим возмущениям.

2.1 Синтез регулятора тока в пространстве естественных координат

Синтез контура тока проведем в пространстве ЭДС преобразователя, тока и скорости. Для этого запишем систему уравнений, описывающую контур тока:

(2.1)

Запишем систему (2.1) в следующем виде:

(2.2)

Перейдём к относительным координатам:

, (2.3)

где- максимально допустимый ток якоря;

- скорость идеального холостого хода;

- максимальная ЭДС преобразователя;

В – максимальное значение управляющего воздействия.

С учётом (2.3) система (2.2) примет вид:

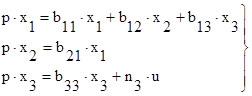, (2.4)

где 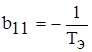, , ,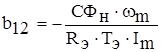