Курсовая работа: Синтез систем подчиненного регулирования

Расчёт коэффициентов системы (2.4) и все дальнейшие расчёты выполнены с помощью программы "Mathcad 11 EnterpriseEdition".

Перейдём к относительным единицам, т.е.

, 2, 3, 4,

где - некоторая стабилизирующая траектория.

В этом случае мы переходим в фазовое пространство возмущённого движения:

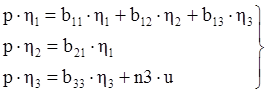(2.5)

Перед нами стоит задача найти управление, ограниченное условием и оптимизирующее функционал вида:

,

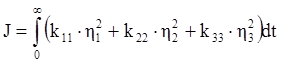где и - корректирующие коэффициенты, ограничивающие координаты и соответственно.

Для решения поставленной задачи необходимо найти функцию Ляпунова, которая является решением функционального уравнения Беллмана:

.

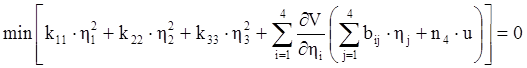В этом случае управление ищется в виде:

,

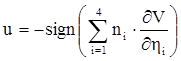где .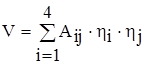

Для определения коэффициентов функции Ляпунова воспользуемся векторным уравнением Барбашина:

(2.6)

где С – матрица Барбашина

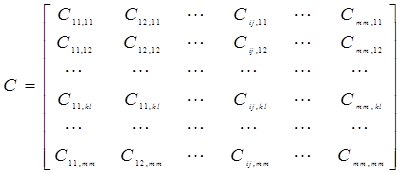
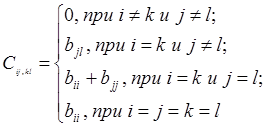(2.7)

А – вектор-столбец коэффициентов Ляпунова;

К – вектор-столбец ограничивающих коэффициентов.

Для нашего случая уравнение (2.6) примет вид:

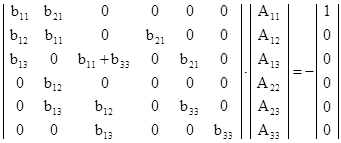
Для данной системы:

Таким образом управление имеет вид:

. (2.8)

В соответствии с (2.8) структурная схема контура тока примет вид, приведенный на рисунке 2.1.

Вычисление коэффициентов A₁₃ , А₂₃ и А₃₃ произведено с помощью программы Mathcad 11 EnterpriseEdition.