Курсовая работа: Синтез систем подчиненного регулирования

Рисунок 2.3 – Структурная схема контура скорости

Функциональная схема регулятора скорости такая же, как и регулятора тока, с той лишь разницей, что регулятор скорости формирует задание на регулятор тока.

В результате меняются лишь сопротивления, причем принимаем, что входное сопротивление R₁₁ =10 кОм, тогда:

(2.18)

Принимаем R₁₂ =20 кОм, R₁₃ =1.5 кОм, R₁₄ =6.8 кОм.

2.3 Синтез регулятора положения

Для облегчения дальнейшего синтеза релейного регулятора положения введем относительные координаты:

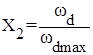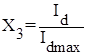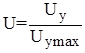;;;;. (2.19)

Приводя замену переменных , (к=1,…,4), преобразуем уравнения в систему дифференциальных уравнений возмущенного движения:

(2.20)

где

Минимальное время отработки заданного перемещения позиционным следящим электроприводом (при наличии ограничений на максимальные значения тока и скорости) может быть обеспечено тогда, когда каждая ограничиваемая координата последовательно от входа к выходу объекта управления будет за минимально возможное время выведена на уровень ограничения и останется застабилизированной на этом уровне до тех пор, пока следующая координата не достигнет заданного значения. Качество управления таким электроприводом может быть задано функционалом:

(2.21)

с изменяющимися в отдельных точках траектории движения системы весовыми коэффициентами W₁₁ , W₂₂ , W₃₃ . Эти точки определяют моменты стыковки законов управления, обеспечивающих оптимальную стабилизацию тока, скорости, положения.

Оптимальное управление, минимизирующее функционал (2.21) на траекториях движения системы (2.20) при ограничении имеет вид:

(2.22)

Коэффициенты А₄₁ , А₄₂ , А₄₃ , А₄₄ являются коэффициентами функции Ляпунова, полная производная во времени которой, вычисленная в соответствии с системой (2.20), равна подынтегральной функции функционала (2.21) с отрицательным знаком.

Построение функции Ляпунова для системы (2.20) приводит к неопределенности, вызванной нулевым корнем характеристического уравнения системы. Этот корень обусловлен наличием в составе силовой части электропривода интегрирующего звена, осуществляющего преобразование угловой скорости вала двигателя в перемещение рабочего органа исполнительного механизма.

Для устранения такого рода неопределенности достаточно представить интегрирующее звено с передаточной функцией в виде звена с передаточной функцией и устремить постоянную времени к бесконечности. При этом справедливо соотношение:

(2.23)

В этом случае расчетная система дифференциальных уравнений возмущенного движения (2.20) видоизменится:

(2.24)

где .

Матричное уравнение Барбашина для синтеза управляющего воздействия релейного регулятора положения примет вид.

Вычисление коэффициентов Ляпунова А₄₁ , А₄₂ , А₄₃ , А₄₄ произведено с помощью прикладной программы MCAD и имеют следующие значения:

В большинстве систем позиционирования желательно обеспечить траектории наибольшего быстродействия, т.е. сформировать прямоугольный график тока, треугольный (трапецеидальный) – скорости и параболический – положения.

Чтобы упростить задатчик, считаем, что переходный процесс позиционирования является процессом второго порядка. Тогда, применительно к данной системе, на траектории наибольшего быстродействия ускорение движения должно изменяться по закону: