Курсовая работа: Система управления положением бортового прожектора вертолёта

Уравнение разомкнутой системы .

.

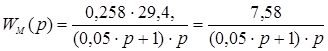Уравнение замкнутой системы:

.

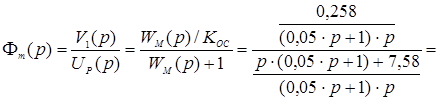
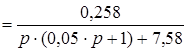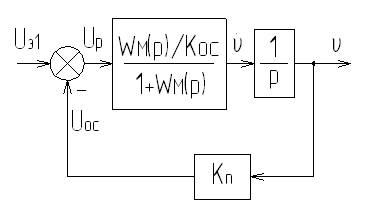
Рис.8 Упрощённая блок-схема первого канала

Запишем окончательную передаточную функцию разомкнутой системы.

;

;

.

Так как , то имеем колебательное звено. Учитывая что , можно пользоваться асимптотическими ЛЧХ колебательного звена, колебания будут малы.

Находим сопрягающую частоту

;

.

На рис. 9 представлены ЛЧХ нескорректированного первого канала.

Рис.9 Нескорректированные ЛЧХ первого канала

По ЛАЧХ видно, что нескорректированная система первого канала устойчива, но предъявленные к систем требования по качеству не выполняются. Кривая ЛАЧХ пересекает ось абсцисс на очень низкой частоте, вследствие чего система имеет очень высокое время регулирования. Путём моделирования нескорректированной системы в среде Matlab было установлено, что время регулирования составляет порядка 15 секунд.

Введём в исследуемую систему корректирующие звенья. Рассчитаем их методом синтеза последовательной коррекции. Найдём желаемую частоту среза, исходя из заданных времени регулирования и величины перегулирования.

Желаемую ЛАЧХ построим исходя из следующих соображений. Среднечастотный участок желаемой ЛАЧХ образуется асимптотой с наклоном , проводимый так, чтобы она пересекала ось частот при . Этот участок проводится влево и вправо до достижения модулей, равных по крайней мере . Высокочастотную область можно пустить параллельно исходной ЛАХ. Низкочастотная область желаемой ЛАЧХ также должна по возможности повторять нескорректированную ЛАЧХ.

Построенная асимптотическая ЛАЧХ находится в приложении к пояснительной записке.

После построения желаемой ЛАЧХ и ЛФЧХ можно строить ЛАЧХ и ЛФЧХ коррекции, исходя из следующих соотношений:

;

;

;