Курсовая работа: Системы связи

Найдем ширину энергетического спектра , используя полученное выражение для энергетического спектра:

.

.

б) Построить в масштабе графики функций корреляции и спектра плотности мощности, отметить на них найденные в пункте а) параметры.

Построим заданную функцию корреляции :

Рис. 2

На этом графике пунктирными линиями обозначено значение интервала корреляции , отложенное в обе стороны от нуля по оси времени.

Построим график спектра плотности мощности , на котором обозначим величину ширины энергетического спектра :

Рис. 3

3. Считая, что исходное сообщение воздействует на идеальный фильтр нижних частот (ИФНЧ) с единичным коэффициентом передачи и полосой пропускания, равной начальной энергетической ширине спектра сообщения:

а) рассчитать среднюю квадратическую погрешность фильтрации (СКПФ) сообщения, среднюю мощность отклика ИФНЧ, частоту и интервал временной дискретизации отклика ИФНЧ

Фильтрация – это линейное преобразование, поэтому отклик ИФНЧ на гауссовское воздействие будет также гауссовским случайным процессом с нулевым математическим ожиданием и мощностью , определяемой по формуле:

.

Количественно эти потери при фильтрации характеризуются средней квадратичной погрешностью фильтрации (СКПФ) :

.

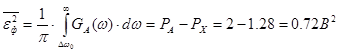Найдем интервал дискретизации:

.

Найдём частоту дискретизации :

.

б) качественно, с учетом найденных в п. а) параметров, изобразить сигналы на входе и выходе дискретизатора АЦП

Сигнал на входе дискретизатора:

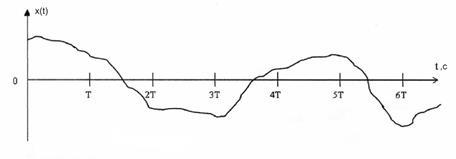Рис. 4

Сигнал на выходе дискретизатора:

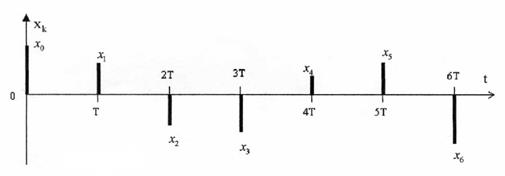
Рис.5

4. Полагая, что последовательность дискретных отсчетов на выходе дискретизатора далее квантуется по уровню с равномерной шкалой квантования:

а) рассчитать интервал квантования, пороги и уровни квантования, среднюю квадратическую погрешность квантования (СКПК).