Курсовая работа: Системы связи

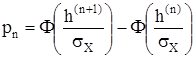, , где -

табулированная функция Лапласа.

n	0	1	2	3	4	5	6	7
	15,6	7,9	2.7	0.3	0.3	2.7	7.9	15.6
	0.0014	0.0214	0.136	0.341	0.341	0.136	0.0214	0.0014

Таблица 5

После суммирования получаем: .

Следовательно, окончательно получаем величину средней квадратической погрешности квантования :

.

4. б) построить в масштабе характеристику квантования

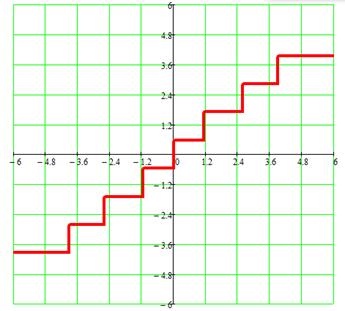Характеристика квантования имеет вид:

Рис. 6

На этом графике по оси абсцисс отложены значения порогов квантования , а по оси ординат – значения уровней квантования .

5. Рассматривая отклик квантователя как случайный дискретный сигнал с независимыми значениями на входе L -ичного дискретного канала связи (ДКС):

а) рассчитать закон и функцию распределения вероятностей квантованного сигнала, а также энтропию, производительность и избыточность L -ичного дискретного источника.

Квантованная последовательность определяется ее одномерным распределением вероятностей вида:

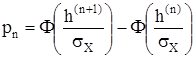, , где -

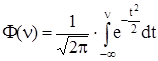табулированная функция Лапласа.

n	0	1	2	3	4	5	6	7
	0.0014	0.0214	0.136	0.341	0.341	0.136	0.0214	0.0014

Таблица 6

Интегральное распределение вероятностей определяется по формуле:

, ; .

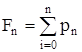Вычислив значения функции распределения , получим:

n	0	1	2	3	4	5	6	7
	0.0014	0.023	0.159	0.5	0.841	0.977	0.998	1

Таблица 7

Рассчитаем энтропию – количество информации, которое должно быть в среднем получено для опознавания любого уровня квантования из их L‑мерного множества:

Производительность или скорость ввода информации в ДКС определяется соотношением:

, где T –

уже найденный интервал временной дискретизации. Зная, что , получим:

.

Избыточность последовательности источника определяется так:

, где –

максимальная энтропия, которая для источника дискретных сообщений равна: