Курсовая работа: Системы связи

, где L = 8 –

число уровней квантования; - среднее квадратическое отклонение отклика ИФНЧ. Значит, шаг квантования :

.

Пороги квантования найдем по формуле:

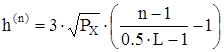, где ,

а крайние пороги, соответственно, равны , а .

Вычислим значения порогов квантования :

n	0	1	2	3	4	5	6	7	8
,В		-3.4	-2.26	-1.13	0	1.13	2.26	3.4

Таблица 2

Теперь найдем уровни квантования из соотношений:

, где ,

Вычислив значения уровней квантования , получим:

n	0	1	2	3	4	5	6	7
, B	-3.95	-2.82	-1.7	-0.56	0.56	1.7	2.82	3.95

Таблица 3

В процессе квантования образуется специфическая погрешность , где – отклик квантователя (значения уровней квантования) на последовательность отсчетов , идущих с выхода дискретизатора. Эта погрешность называется шумом квантования.

Найдем среднюю квадратическую погрешность квантования (или мощность шума квантования):

, где и –

соответственно, мощности (дисперсии) входного и выходного сигналов квантователя, а – коэффициент взаимной корреляции между этими сигналами.

Вычислили, что . Найдем коэффициент взаимной корреляции:

,

где коэффициент рассчитывается по формуле:

.

В этой формуле необходимо просуммировать значения ФПВ нормальной случайной величины:

,

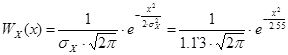где в качестве аргумента выступают найденные значения порогов квантования. Найдем эти значения ФПВ для различных значений порогов квантования:

,В	-3.4	-2.26	-1.13	0	1.13	2.26	3.4
	0.0037	0.048	0.214	0.353	0.214	0.048	0.0037

Таблица 4

Просуммируем найденные значения и найдем :

.

Значит, .

Теперь найдем мощность выходного сигнала квантователя по формуле:

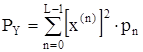, где