Курсовая работа: Системы связи

.

Мощность сигнала ДОФМ и амплитуда , в среднем приходящаяся на один двоичный символ:

-мощность сигнала ДОФМ на один двоичный символ.

-амплитуда сигнала ДОФМ на один двоичный символ.

Пропускная способность характеризует максимально возможную скорость передачи информации по данному каналу. Пропускная способность гауссовского НКС определяется по формуле:

.

б) построить в масштабе четыре графика функций плотности вероятностей (ФПВ) мгновенных значений и огибающих узкополосной гауссовской помехи (УГП) и суммы гармонического сигнала с УГП

ФПВ мгновенных значений УГП имеют вид гауссовского распределения с числовыми характеристиками: нулевым математическим ожиданием и дисперсией (мощностью) .

ФПВ мгновенных значений УГП задается соотношением вида:

.

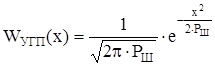ФПВ мгновенных значений суммы гармонического сигнала с УГП равна:

.

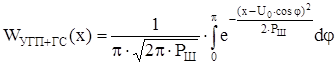Построим графики полученных выражений для ФПВ мгновенных значений УГП и суммы гармонического сигнала и УГП:

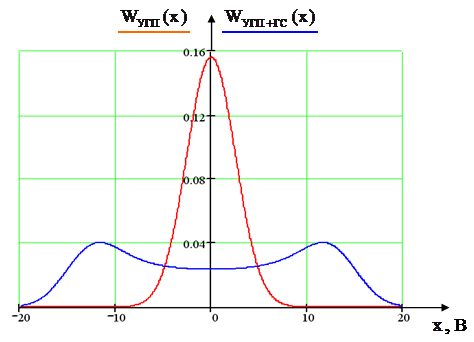1/В

Рис. 11

Огибающая гауссовской помехи распределена по закону Рэлея:

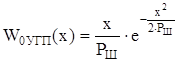, при .

Огибающая суммы гармонического сигнала и УГП подчиняется обобщенному распределению Рэлея (распределению Райса):

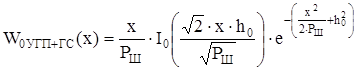, при ,

где – модифицированная функция Бесселя нулевого порядка от мнимого аргумента.

Построим графики полученных выражений для огибающих УГП и суммы гармонического сигнала и УГП:

1/В

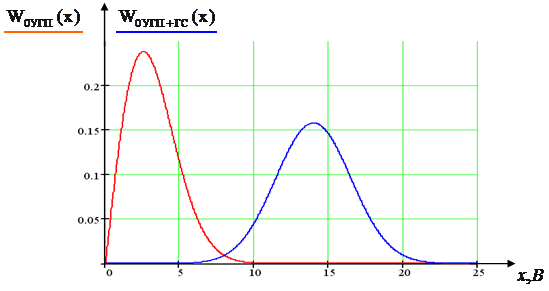
Рис.12

9. С учетом заданного вида приема (детектирования) сигнала дискретной модуляции:

а) рассчитать среднюю вероятность ошибки в двоичном ДКС, скорость передачи информации по двоичному симметричному ДКС, показатель эффективности передачи сигнала дискретной модуляции по НКС

За количественную меру помехоустойчивости в системах электросвязи принимается средняя на бит вероятность ошибки:

, где и – безусловные (априорные) вероятности передачи 1 и 0.

При равенстве априорных вероятностей , а также условных вероятностей (условие симметричности двоичного ДКС), средняя на бит вероятность ошибки равна .