Курсовая работа: Сравнительный анализ численных методов

;

<- необходимая точность достигнута, итерационный процесс можно останавливать.

Добиться указанной точности нам удалось на 3-й проведенной итерации

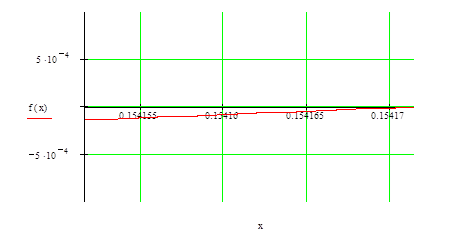
Рисунок 4. График функции на отрезке [; ]

Наименьшим полученным отрезком, в котором содержится корень уравнения является

[; ].

Значения исходной функции на концах этого отрезка

f()=-0,0001391

f()=0,000000033

Как мы видим, на каждой итерации объем вычислений в методе касательных больший, чем в методе хорд, так как приходится находить не только функции F(х) , но и ее производной. Однако скорость сходимости значительно выше в методе касательных: в методе касательных условие сходимости выполнилось на 3- м шаге, а в методе хорд на 5-м.

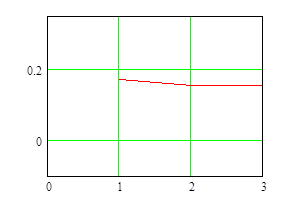
Рисунок 5. График функции для метода касательных

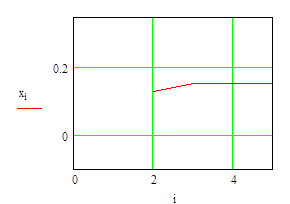
Рисунок 6. График функции для метода хорд

Говоря о функции х=, - выбрав начальное приближение х0 (для метода касательных), х0 и x1(для метода хорд) строится последовательность хn стремящаяся к и условием сходимости здесь является ,т.е. тангенс угла наклона касательной должен быть меньше 1(угол должен составлять менее 45 градусов). Исходя из рисунков 5,6 очевидно что условие сходимости () итерационной процедуры было выполнено.

1.5 Программная реализация итерационных методов

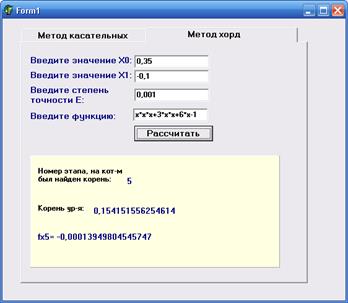
Рисунок 7. Решение уравнения методом хорд

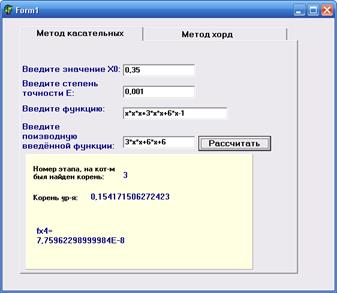
Рисунок 8. Решение уравнения методом касательных

Раздел 2. Интерполирование

Одним из основных типов точечной аппроксимации является интерполирование. Оно состоит в следующем: для данной функции строим интерполирующую функцию φ(х), принимающую в заданных точках , те же значения , что и функция , т.е.