Курсовая работа: Сравнительный анализ численных методов

При этом предполагается, что среди значений нет одинаковых, т.е. при . Точки называются узлами интерполяции.

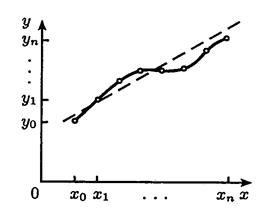
Рисунок 9. Интерполяция.

Таким образом, близость интерполирующей функции (сплошная линия) к заданной функции состоит в том, что их значения совпадают на заданной системе точек. Интерполирующая функция φ(х) может строиться сразу для всего рассматриваемого интервала измерения х или отдельно для разных частей этого интервала. В первом случае говорят о глобальной интерполяции, во втором – о кусочной (или локальной) интерполяции.

2.1 Многочлен Лагранжа

Рассмотрим случай глобальной интерполяции, т.е. построение интерполяционного многочлена, единого для всего отрезка .

Будем искать интерполяционный многочлен в виде линейной комбинации многочленов степени n:

При этом потребуем, чтобы каждый многочлен обращался в нуль во всех узлах интерполяции, за исключением одного (i-го), где он должен равняться единице. Этим условиям при i=0 отвечает многочлен вида

.

По аналогии получим

при i=1

,

при i=2

,

,

Подставляя полученные выражения в

,

находим

.

Эта формула определяет интерполяционный многочлен Лагранжа.

Обратное интерполирование заключается в установлении зависимости . Задача обратного интерполирования заключается в том, чтобы по заданному значению функции y определить соответствующее значение аргумента x.

Функция выглядит следующим образом:

Ln(y)=

2.2 Практическое применение метода интерполяции для решения уравнений

Для исследования примем ту же функцию , что и в предыдущем разделе: