Курсовая работа: Свойства многоугольников и их применение в решении задач

Свойства параллелограмма:

1) противолежащие стороны равны;

2) противоположные углы равны;

3) диагонали точкой пересечения делятся пополам;

4) сумма углов, прилежащих к одной стороне, равна 180°;

5) сумма квадратов диагоналей равна сумме квадратов всех сторон: d₁ ² +d₂ ² =2(a² +b² ). (3.3)

6) Около параллелограмма можно опи­сать окружность тогда и только тогда, когда этот параллелограмм является прямоугольником.

7) Если параллелограмм вписан в окружность, то он является ромбом.

Признаки параллелограмма:

Четырехугольник является параллелограммом, если:

1. Две его противоположные стороны равны и параллельны.

2. Противоположные стороны попарно равны.

3. Противоположные углы попарно равны.

4. Диагонали точкой пересечения делятся пополам.

3.2. ТРАПЕЦИЯ. СВОЙСТВА И ПРИЗНАКИ ТРАПЕЦИИ

Трапецией называется четырехугольник, у которого две противолежащие стороны параллельны, а две другие 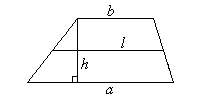непараллельны.

Параллельные стороны трапеции называются ее основаниями, а непараллельные стороны — боковыми сторонами. Отрезок, соединяющий середины боковых сторон, называется средней линией.

Трапеция называется равнобедренной (или равнобокой), если ее боковые стороны равны.

Трапеция, один из углов которой прямой, называется прямоугольной.

Свойства трапеции:

1 ее средняя линия параллельна основаниям и равна их полусумме;

2 если трапеция равнобокая, то ее диагонали равны и углы при основании равны;

3 если трапеция равнобокая, то около нее можно описать окружность;

4 если сумма оснований равна сумме боковых сторон, то в нее можно вписать окружность.

5 Площадь трапеции:
a и b — основания; h — расстояние между ними; l — средняя линия
, S = lh (3.4)

6 Около трапеции можно описать ок­ружность тогда и только тогда, когда эта трапеция равнобедренная.

Признаки трапеции:

Четырехугольник является трапецией, если его параллельные стороны не равны

3.3. ПРЯМОУГОЛЬНИК. ЕГО СВОЙСТВА И 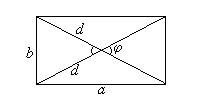ПРИЗНАКИ

Прямоугольником называется параллелограмм, у которого все углы прямые.

Свойства прямоугольника:

1 все свойства параллелограмма;

2 диагонали равны.