Курсовая работа: Свойства многоугольников и их применение в решении задач

Т.к. ABCD прямоугольник, то BD=AC. Тогда И . Приравняем полученные равенства:

= .

Задача2 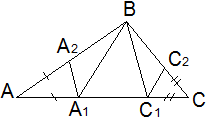AC – наибольшая сторона треугольника ABC . На АС выбираются точки А₁ и С₁ так, что АС₁ =АВ и СА₁ =СВ . Затем на стороне АВ берется точка А₂ так, что АА₁ =АА₂ , а на стороне CD – точка С₂ так, что СС₁ =СС₂ . Докажите, что точки А₁ , А₂ , С₁ , С₂ лежат на одной окружности.

РЕШЕНИЕ: АА₁ =АА₂ и АС₁ =АВ (по условию задачи), а тока А₁ и А₂ A ₁ A ₂ || BC ₁ ? При чем по теореме Фалеса. Можно сделать вывод, что A ₁ A ₂ BC ₁ равнобокая трапеция. Аналогично можно доказать, что четырехугольник A ₁ ВС₂ С₁ также равнобокая трапеция. Так как эти трапеции правильные, то около них можно описать окружности и соответственно. Мы получили, что точки A ₁ , В и С₁ принадлежат двум окружностям одновременно, что невозможно, т.к. по свойству окружности: через три точки может проходить только одна окружность. Тогда можно сделать вывод о том, что и совпадают. А следовательно точки А₁ , А₂ , С₁ , С₂ лежат на одной окружности.

Задача3 Докажите, что выпуклый n -угольник является правильным тогда и только тогда, когда он переходит в себя при повороте на угол вокруг некоторой точки.

РЕШЕНИЕ: Выпуклый n -угольник называется правильным, если все его стороны равны и все углы равны. Пусть A ₁ A ₂ ...A _n -- правильный многоугольник, O — точка пересечения биссектрис его углов A _n A ₁ A ₂ и A ₁ A ₂ A ₃ . Тогда треугольники A _n OA ₁ и A ₂ OA ₁ равны по двум сторонам и углу между ними.

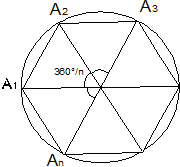Кроме того, из равенства углов n -угольника следует, что треугольники A _n OA ₁ A ₂ OA ₁ — равнобедренные. Поэтому

OA _n = OA ₁ = OA ₂ , A _n OA ₁ = A ₁ OA ₂ .

Аналогично докажем, что

OA ₁ = OA ₂ =...= OA _n ,A ₁ OA ₂ = A ₂ OA ₃ =...= =A _n OA ₁ = .

Следовательно, O — центр окружности, проходящей через точки A ₁ , A ₂ , ..., A _n . При повороте на угол вокруг точки O данный n -угольник переходит сам в себя.

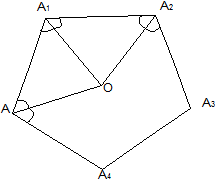
Пусть теперь известно, что некоторый выпуклый n -угольник A ₁ A ₂ ...A _n переходит в себя при повороте вокруг некоторой точки O на угол . Ясно, что эта точка лежит внутри многоугольника, а т.к. многоугольник выпуклый, то

A ₁ OA ₂ +...+ A _n OA ₁ = 360^o .

Поскольку вершины многоугольника при повороте переходят в вершины, то точки A ₁ , A ₂ , ..., A _n лежат на окружности с центром O , и

A ₁ OA ₂ = A ₂ OA ₃ =...= A _n OA ₁ = .

Поэтому A ₁ OA ₂ , A ₂ OA ₃ , ..., A _n OA ₁ — равные равнобедренные треугольники. Следовательно, все стороны и все углы многоугольника равны, т.е. он правильный.

Задача4 Докажите, что в правильном 12-угольнике A ₁ A ₂ ...A ₁₂ диагонали A ₁ A ₅ , A ₂ A ₆ , A ₃ A ₈ и A ₄ A ₁₁ пересекаются в одной точке.

РЕШЕНИЕ:

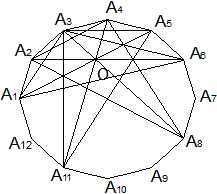Пусть A ₁ A ₂ ...A ₁₂ — правильный 12-угольник. Рассмотрим треугольник A ₂ A ₄ A ₈ . Прямые A ₂ A ₆ , A ₃ A ₈ и A ₄ A ₁₁ — биссектрисы его углов. Точно так же прямые A ₃ A ₈ , A ₅ A ₁ и A ₁₁ A ₄ — биссектрисы углов треугольника A ₃ A ₅ A ₁₁ . Отсюда следует, что диагонали A ₁ A ₅ , A ₂ A ₆ , A ₃ A ₈ и A ₄ A ₁₁ проходят через одну точку.

Задача5 Пусть О — центр правильного многоугольника A₁ A₂ A₃ ...A_n , X -- произвольная точка плоскости. Докажите, что:

a) +...+ = 0

б) +...+ = n.

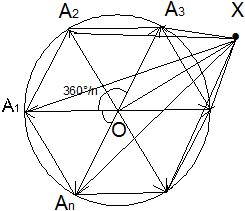РЕШЕНИЕ:

а) Обозначим +...+ = . При повороте на угол вокруг точки O точка переходит в точку (1i n - 1), а точка A_n — в точку A₁ . Поэтому вектор при таком повороте переходит сам в себя. Следовательно, =0 .

б)

Задача6 Докажите, что сумма расстояний от произвольной точки X до вершин правильного n -угольника будет наименьшей, если X — центр n- угольника.

РЕШЕНИЕ:

Пусть X_k — образ точки X при повороте относительно центра O данного n- угольника, переводящем A_k в A₁ . При этом повороте отрезок A_k X переходит в A₁ X_k . Следовательно, A₁ X + ... + A_n X = A₁ X₁ + ... + A₁ X_n . А так как n- угольник X₁ ...X_n правильный, то + ... + = n (см. Задачу5), а значит, A₁ X₁ + ... + A_n X_n n.

Задача7 В правильном n -угольнике (n 3) отмечены середины всех сторон и диагоналей. Какое наибольшее число отмеченных точек лежит на одной, окружности?