Курсовая работа: Свойства многоугольников и их применение в решении задач

S = ab (3.5)

S = d ₁ d ₂ sin (3.6)

4 если прямоугольник вписан в окружность, то он является квадратом.

Признаки прямоугольника:

Параллелограмм является прямоугольником, если:

1. Один из его углов прямой.

2. Его диагонали равны.

3.4. РОМБ. ЕГО СВОЙСТВА И ПРИЗНАКИ

Ромбом называется параллелограмм, у которого все стороны равны.

Свойства ромба:

1 все свойства параллелограмма;

2 диагонали перпендикулярны;

3 диагонали являются биссектрисами его углов.

4 площадь ромба:

S = ah_a (3.7)

S = a² sin (3.8)

S =d₁ d₂ (3.9)

Признаки ромба:

1. Параллелограмм является ромбом, если:

2. Две его смежные стороны равны.

3. Его диагонали перпендикулярны.

4. Одна из диагоналей является биссектрисой его угла.

3.5. КВАДРАТ. ЕГО СВОЙСТВА И ПРИЗНАКИ

Квадратом называется прямоугольник, у которого все 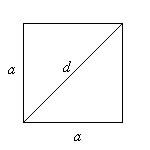стороны равны.

Свойства квадрата

1 все углы квадрата прямые;

2 диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.

3 площадь квадрата:

S = a² (3.10)

S = d ² (3.11)

Признаки квадрата:

Прямоугольник является квадратом, если он обладает каким-нибудь признаком ромба.

4.ПРИМЕРЫ РЕШЕННЫХ ЗАДАЧ.

Задача1 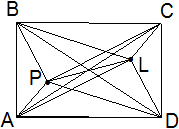Точка Р лежит внутри прямоугольника ABCD . Докажите, что .

РЕШЕНИЕ: Рассмотрим параллелограммы BLDP и APCL: по свойству d₁ ² +d₂ ² =2(a² +b² ) получим