Курсовая работа: Теория автоматического управления
Рис. 1.3.4
Полученный годограф начинается на вещественной положительной полуоси, проходит 2 квадранта в отрицательном направлении, таким образом, критерий Михайлова не выполняется, следовательно, система неустойчива.
2. Построение области устойчивости в плоскости параметра Кр
Построим область устойчивости, используя критерий Гурвица.
Запишем характеристическое уравнение замкнутой системы в общем виде:
![]() .
.
![]()
![]()
Для конкретного случая характеристическое уравнение замкнутой системы имеет вид:
![]() (11)
(11)
Для устойчивости системы КР должно удовлетворять необходимому условию
![]()
![]()
Рис. 2.1
Но заметим, что исходный КР удовлетворяет этому условию, и его изменением устойчивости замкнутой системы добиться невозможно, т. к. в ХУ ЗС (2.3) а2 <0, и зависит этот коэффициент от постоянных времени.
Построим область устойчивости в плоскости параметра Т2
Необходимое условие устойчивости:
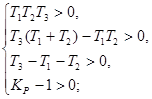
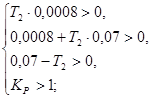
Достаточное условие устойчивости для системы третьего порядка по критерию Гурвица имеет вид:
![]()
![]()
![]()
![]()
![]()
Учитывая все условия:
![]()
![]()
Рис. 2.2
3. Коррекция системы
Для обеспечения устойчивости системы необходимо ввести корректирующее звено с передаточной функцией вида:
![]()
Структурная схема скорректированной системы (Рис. 3.1):