Курсовая работа: Види розподілу ймовірностей й оцінка його параметрів
1.1 Біномінальний розподіл
Нехай виробляється п незалежних іспитів, у кожнім з який подія А може з'явитися, або не з'явитися. Імовірність настання події у всіх іспитах постійна і дорівнює р (отже, імовірність непояви q=l-p). Розглянемо в якості дискретної випадкової величини Xчисло появ події А в цих іспитах.
Поставимо перед собою задачу: знайти закон розподілу величини X. Для її рішення потрібно визначити можливі значення X і їхньої імовірності.
Очевидно, подія А у п іспитах може або не з'явитися, або з'явитися 1 раз, або 2 рази,..., або п раз. Таким чином, можливі значення Xтакі:
![]()
Залишається знайти імовірності цих можливих значенні, для чого досить скористатися формулою Бернуллі:
![]() (1.1)
(1.1)
де ![]() =0, 1, 2,..., п .
=0, 1, 2,..., п .
Формула (1.1) і є аналітичним вираженням шуканого закону розподілу. Біномінальним називають розподіл ймовірностей, обумовлений формулою Бернуллі.
Закон названий "біномінальним" тому, що праву частину рівності (1.1) можна розглядати як загальний член розкладання бінома Ньютона
![]() (1.2)
(1.2)
Таким чином, перший член розкладання ![]() визначає імовірність настання розглянутої події п раз у п незалежних, іспитах; другий член
визначає імовірність настання розглянутої події п раз у п незалежних, іспитах; другий член ![]() визначає імовірність настання події п -1 раз;...; останній член
визначає імовірність настання події п -1 раз;...; останній член ![]() визначає імовірність того, що подія не з'явиться жодного разу. Напишемо біномінальний закон у виді таблиці:
визначає імовірність того, що подія не з'явиться жодного разу. Напишемо біномінальний закон у виді таблиці:
![]()
Приклад:
Монета кинута 2 рази. Написати у виді таблиці закон розподілу випадкової величини X- числа випадань герба.
Рішення:
Імовірність появи герба в кожнім киданні монети ![]() отже, імовірність не появи герба:
отже, імовірність не появи герба:
![]()
При двох киданнях монети герб може з'явитися або 2 рази, або 1 раз, або зо всім не з'явитися. Таким чином, можливі значення Xтакі:
![]()
Знайдемо імовірності цих можливих значенні по формулі Бернуллі:
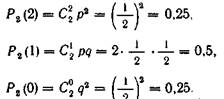
Напишемо шуканий закон розподілу:
![]()
Контроль:
![]()
1.2 Розподіл Х ²
Нехай ![]() (і=1,2,...,п) - нормальні незалежні випадкові величини, причому математичне чекання кожної з них дорівнює нулю, а середнє квадратичне відхилення - одиниці. Тоді сума квадратів цих величин
(і=1,2,...,п) - нормальні незалежні випадкові величини, причому математичне чекання кожної з них дорівнює нулю, а середнє квадратичне відхилення - одиниці. Тоді сума квадратів цих величин