Курсовая работа: Види розподілу ймовірностей й оцінка його параметрів

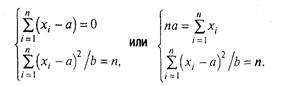
Перевіримо достатні умови максимуму функції In L у точці (а*, b*).

Знайдемо:

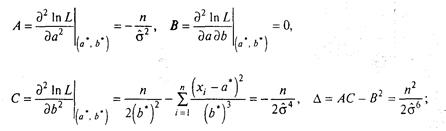
тому що ∆ >0, А<0, то крапка (а * = ,b *= ] є крапкою максимуму функції In L. Тому оцінки максимальної правдоподібності =х, =. Оцінки збіглися з оцінками методу моментів.

Приклад 3.2.2 Знайдемо методом максимальної правдоподібності оцінки параметрів а і bрівномірного на відрізку [а,b] розподіли. Відповідно до формули (3.15), функція правдоподібності

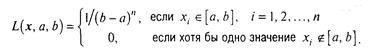
При першій умові система (3.18) не розв'язна, при другому - не визначена. Оцінки і варто шукати на границі області припустимих значень для а і b:

де а . Тоді умова (3.16) прийме вид:

Тому що функція L(a,b) =1/(b - а)" убуває при зростанні bи убуванні а, то її максимум на області {} досягається в точці .

Приклад 3.2.4 Випадковий розмір Х- число успіхів в одиничному випробуванні: Р(Х = х) = р^х (1 – р) ^1-х , х = 0,1; р - імовірність успіху в одиничному випробуванні. Знайдемо оцінку максимальної правдоподібності розташовуючи вибіркою х₁ , х₂ ..., х_п , де х_і - число успіхів у і -м випробуванні.

де т - число успіхів у л випробуваннях Бернуллі (таку ж оцінку можна одержати і методом моментів). Ця оцінка заможна, незміщена і, у чому неважко переконатися, ефективна.

Відзначена вище природність визначення оцінок максимальної правдоподібності з умови (3.16) підкріплюється їхніми гарними властивостями. Якщо функція щільності fx (х, 9) (функція імовірності Р(Х = х, 9), якщо-дискретна) задовольняє досить загальним умовам регулярності, оцінка максимальної правдоподібності має при великих я розподіл, близький до нормального з математичним чеканням, рівним , і дисперсією, рівної 1/[пІ ()], де І() визначається співвідношенням (3.9), є заможної, асимптично несумісної і асимптично ефективної; більш того, якщо існує ефективна оцінка параметра, вона буде єдиним вирішенням рівняння максимальної правдоподібності.

Крім описаних методів оцінювання параметрів існує ряд інших, наприклад метод найменших квадратів, відповідно до котрого

оцінка параметра знаходиться з умови:

(3.19)

Звернемо увагу на те, що математичного чекання нормального розподілу з відомим значенням дисперсії умова (3.19) ідентично умові методу максимальної правдоподібності (3.16).

В останні роки розвиваються так називані робастні, або стійкі, методи оцінювання, що дозволяють знаходити оцінки, хоча і є не найкращими в рамках передбачуваного закону розподілу, але має досить стійкі властивості при відхиленні реального закону від передбачуваного.

3.2 Поняття інтервальної оцінки. Інтервальні оцінки параметрів нормального розподілу

Обчислена на основі вибірки оцінка є лише наближенням до невідомого значення параметра навіть у тому випадку, коли ця оцінка заможна, незміщена й ефективна. Виникає питання: не можна чи зазначити таке А, для якого з заздалегідь заданої близької до одиниці імовірністю 1 - α гарантувалося б виконання нерівності: |-| < ∆, або інакше, для котрого

(3.2.1)

Якщо таке А існує, то інтервал (-∆, +∆) називають іньервальної оцінкою параметра 9, або довірчим інтервалом; -∆, + ∆ — нижньої і верхньої довірчими границями; ∆ — помилкою оцінки , 1-α — надійністю інтервальної оцінки, або довірчою імовірністю. Вибір довірчої імовірності визначається конкретними умовами; звичайно використовуються значення 1 - α, рівні 0,90; 0,95; 0,99.

Оцінка , будучи функцією випадкової вибірки, є випадковим розміром, ∆ також випадкова: її значення залежить від імовірності 1 - α і, як правило, від вибірки. Тому довірчий інтервал випадковий і вираження (3.2.1) варто читати так: «Інтервал (-∆, +∆ накриє параметр з імовірністю 1 — α», а не так: «Параметр потрапить у інтервал (-∆, +∆ з імовірністю 1 - α».

У формулі (3.2.1) границі довірчого інтервалу симетричні щодо крапкової оцінки. Однак не завжди вдасться побудувати інтервал, що володіє такою властивістю. Для одержання довірчого інтервала найменшої довжини при заданому об'ємі виборки п і заданої довірчої імовірності 1 - а в якості оцінки параметра варто брати ефективну або асимптотично ефективну оцінку.

Існує два підходи до побудови довірчих інтервалів.