Курсовая работа: Види розподілу ймовірностей й оцінка його параметрів

звідси одержимо, що при п - P(/-/<)1.

Уведемо поняття ефективності й асимптотичної ефективності незміщеної оцінки скалярного параметра .

Ефективністю е() незміщеної оцінки параметра називають відношення min DQn( є s)— мінімально можливого значення дисперсії оцінки в класі S всіх незміщених оцінок параметра до дисперсії Dn розглянутої оцінки. При виконанні функцією щільності f_х (х, 0) [функцією імовірності Р(Х =х, )] досить загальних умов регулярності: дифференційованих по , незалежності області визначення від і т. д. — має місце нерівність Рао—Крамера—Фреше:

(3.8)

де i() — кількість інформації про параметр , що міститься в одиничному спостереженні, визначається співвідношенням

(3.9)

(i() — деяка постійна, що залежить від ). Тому

(3.10)

якщо е() = 1, то — ефективна оцінка параметра у класі S усіх

його незміщенних оцінок.

Асимптотичної ефективністю оцінки називають розмір

(3.11)

якщо () = 1 то — асимптотична ефективна оцінка (очевидно, що ефективна оцінка буде й асимптотично ефективною). Знайдемо вираження для асимптотичної ефективності оцінки

. Тому що при великих п оцінку можна вважати незміщеною, то з урахуванням формул (3.11,3.10,3.7) одержимо

Приклад 3.1.3 Переконаємося в тому, що знайдена методом моментів по випадковій вибірці з генеральної сукупності X ~ N (а, а) оцінка X параметра а є ефективної в класі не зміщених оцінок, а оцінка ² параметра ² є, після виключення зміщення, асимптотично ефективною.

Оцінка X - незміщена, і DX = ² /п. Припустивши, що ² відома, і використовуючи формулу (3.10), у якій, з обліком нормальності розподілу,

1(а) = М(dln f(x,a)/da) = 1/ ² одержимо, що е() = 1. Звідси X - ефективна оцінка.

Оцінка - зміщена; виключивши зміщення, одержимо оцінку

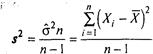
дисперсія котрої Ds =2/n-1 .

Припустивши, що а відомо, і використовуючи вираження (3.10), у котрому, с обліком нормальності розподілу,

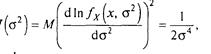
одержимо, що ефективність е(s2) =(n – 1/n)<1, а асимптотична эффективність e0(s2) = lime(s2) = 1. Отже, s2 – асимптотична эффективна оцінка.

Зауваження.

Незміщеною і ефективною оцінкою дисперсії є використовувана при відомому значенні параметра а оцінка s = (Xі -a) / п, тому що Мs = ² , Ds = 2/n и е(s) = 1.

При виконанні досить загальних умов усі три оцінки: ² ,s² і s забеспечені.

У приведеному прикладі оцінки методу моментів X і ² є відповідно ефективної й асимптотично ефективної. Однак подібні приклади швидке виключення: набагато частіше оцінки методу моментів із погляду ефективності не є найкращими з можливих навіть при великих п. Р. Фишер показав, що асимптотична ефективність цих оцінок часто значно менше одиниці. Асимптотично ефективні оцінки можуть бути отримані методом максимальної правдоподібності.