Курсовая работа: Види розподілу ймовірностей й оцінка його параметрів

В основі методу максимальної правдоподібності лежить поняття функції правдоподібності. Нехай Х= (Х, Х₂ ,..., Х_п ) — випадкова, а х = (х,х,..., х_п ) — конкретна вибірки з генеральної сукупності X. Нагадаємо, випадкової називають вибірку, що задовольняє наступним умовам:

випадкові розміри Х, Х₂ ,,.., Х_п незалежні, тобто

(3.12)

(3.13)

розподіл кожною з розмірів Х збігається з розподілом розміру X, тобто при і= 1, 2,..., n.

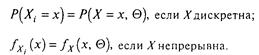(3.14)

Функція правдоподібності — це функція L (х, ), значення якої в точці х визначається співвідношенням:

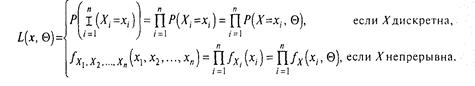
З визначення випливає: чим ймовірніше при фіксованому набір х, тим більше значення функції правдоподібності L (x, ), звідси і її назва.

Отже,

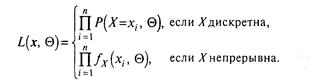(3.15)

Відповідно до методу максимальної правдоподібності оцінка максимальної правдоподібності ^(п) = (^п) , ,..., ) параметра = (, ,..., ), при заданому наборі х визначається з умови:

(3.16)

де {} - область припустимих значень для .

Природність такого підходу до визначення оцінки випливає зі змісту функції L: при фіксованому функція L (х, 0) — міра правдоподібності набору х; тому, змінюючи , можна простежити, при яких його значеннях набір є більш правдоподібним, а при яких - менше, і вибрати таке значення , при якому наявний набір х буде найбільш правдоподібним.

У ряді випадків зручніше визначати з умови:

In £(х, ) = In L(x, ) (3.17)

ідентичного умові (3.16): якщо замість функції L узяти In L, крапка максимуму не зміниться. Функцію In L (х, 0) називають логарифмічною функцією правдоподібності.

Відповідно до формули (3.17), для знаходження ^(П) випливає: знайти вирішення системи рівнянь максимальної правдоподібності

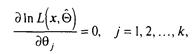(3.18)

при цьому вирішенням вважається лише такий набір * = (*,*,..., *), що задовольняє (3.18), у якому кожне * дійсно залежить від х;

серед вирішень, що лежать усередині області {}, виділити крапки максимуму;

якщо система (3.18) не визначена, не розв'язна або якщо серед її вирішень немає крапки максимуму усередині {}, то крапку максимуму варто шукати на границі області {}.

Приклад 3.2.1 Знайдемо методом максимальної правдоподібності оцінки параметрів а і b = σ ² нормального розподілу.

Відповідно до формули (3.15), функція правдоподібності

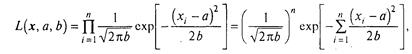
логарифмічна функція правдоподібності

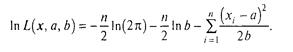
Приватні похідні: