Лабораторная работа: Амплитудная модуляция смещением

3.2.2 Спектр периодической последовательности видеосигналов

Периодический сигнал может быть представлен рядом Фурье:

, (3.7)

где X[n] – коэффициенты ряда Фурье.

(3.8)

Согласно выражениям (3.8) и (3.9) периодический сигнал состоит из суммы бесконечного числа гармонических колебаний кратных частот (гармоник), вклад которых в общую сумму определяется весовыми коэффициентами X[n]. Таким образом, являясь амплитудами дискретных частотных компонентов (гармоник) составляющих данный сигнал, коэффициенты X[n] образуют дискретный спектр периодического сигнала рисунок 3.4. «Востановленный» с помощью ряда Фурье сигнал, при суммировании десяти первых гармоник, приведен на рис 3.5.

Рисунок 3.4 - Спектр периодического сигнала.

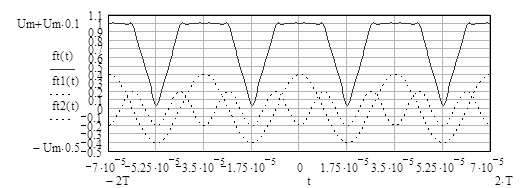
Рисунок 3.5 - Сигнал представленный рядом Фурье, первая и вторая гармоники (пунктирные линии).

3.3 Радиосигнал

3.3.1 Математическая модель радиосигнала

Радиосигнал с огибающей в форме видеосигнала находим из соотношения:

, (3.9)

где

- математическая модель радиосигнала, В;

f₀ - частота несущего высокочастотного колебания, Гц;

- начальная фаза колебания, рад.

Найдем частоту несущего высокочастотного колебания f_0, которая совпадает с резонансной частотой колебательного звена:

(3.10)

где

- индуктивность колебательного звена, Гн,

- значение емкости колебательного звена, Ф.

Подставляя численное значение частоты несущего высокочастотного колебания (f₀ =918,9 кГц), в (3.9) построим график радиосигнала рисунок 3.6.

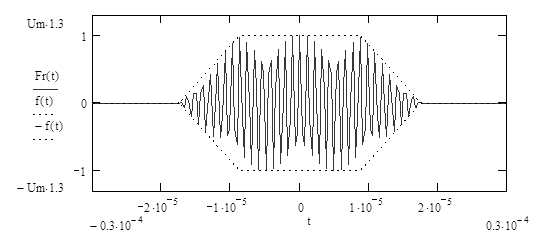
Рисунок 3.6 - Радиосигнал

3.3.2 Спектр радиосигнала

Для отыскания спектральной плотности радиосигнала воспользуемся соотношением:

, (3.11)