Лабораторная работа: Амплитудная модуляция смещением

- спектральная плотность видеосигнала (3.5) на соответствующих частотах, В;

Таким образом, подставляя в выражение (3.11) аналитическое выражение для спектральной плотности видеосигнала (3.5) , и принимаем .

Графическое изображение спектральной плотности радиосигнала приведено на рисунок 3.7. Как видно, при достаточно большом значении частоты несущего высокочастотного колебания, спектральная плотность радиосигнала представляет собой две симметричные копии спектра видеосигнала с половинной амплитудой перенесенные на частоту несущего колебания.

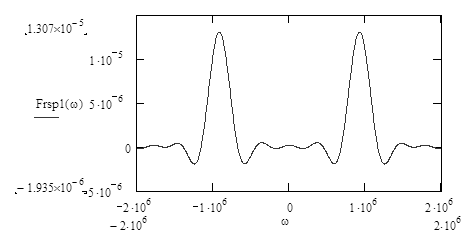
Рисунок 3.7 - Спектральная плотность радиосигнала

3.4 Аналитический сигнал, соответствующий радиосигналу

Аналитический сигнал, соответствующий реальному физическому сигналу , определяется соотношением:

, (3.12)

где

- функция, сопряженная по Гильберту выходному сигналу;

- реальный физический сигнал.

. (3.13)

Также аналитический сигнал может быть представлен через модуль аналитического сигнала

, (3.14)

и полную фазу (3.15)

в виде (3.16)

Для радиосигнала полную фазу можно записать в форме:

, (3.17)

где w₀ - частота несущего высокочастотного колебания, ;

Q(t) - изменяющаяся во времени фаза, рад; Q₀ - постоянная во времени начальная фаза, рад. В этом случае аналитический сигнал определяется соотношением:

, (3.18)

где

-комплексная огибающая аналитического сигнала, соответствующего радиосигналу, В;

Заметим, что комплексная огибающая аналитического сигнала вещественна, то есть не имеет мнимой составляющей и представляет собой видеосигнал (3.2). Поэтому аналитический сигнал, соответствующий радиосигналу можно представить:

Спектральная плотность аналитического сигнала сосредоточена только в области положительных частот и находится из соотношения:

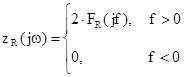, (3.19)

где

- спектральная плотность радиосигнала (3.11)