Лабораторная работа: Амплитудная модуляция смещением

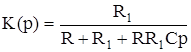. (4.3)

4.1.3 Импульсная характеристика апериодического звена

Импульсная характеристика цепи определяется как реакция цепи на входной сигнал в виде дельта-функции.

Импульсная характеристика находится ОПЛ от операторного коэффициента передачи. ОПЛ определяется следующим образом:

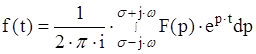. (4.4)

Однако на практике при расчетах операторным методом пользуются таблицами прямых и обратных преобразований Лапласа. Это в значительной мере облегчает вычисления. Вычислив обратное преобразование Лапласа от операторного коэффициента передачи его получим:

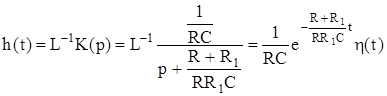. (4.5)

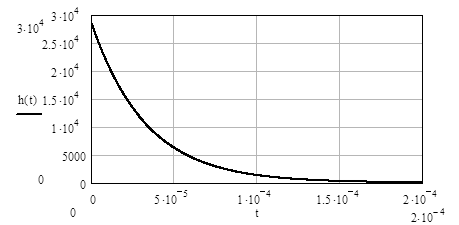
Рисунок 4.4– Импульсная характеристика апериодического звена

4.1.4 Переходная характеристика апериодического звена

Переходная характеристика цепи представляет собой реакцию цепи на сигнал в виде функции Хевисайда. В общем случае переходная характеристика находится как:

, (4.6)

где L ^-1 – обратное преобразование Лапласа.

Вычислив выражение (4.6) получим:

. (4.7)

Рисунок 4.5– Переходная характеристика апериодического звена

4.2 Исследование колебательного звена

R1

Рисунок 4.6 - Схема электрическая принципиальная колебательного звена

L=1.5 мкГн

С=20.000 пФ

Q=50

Для последовательного колебательного контура справедлива формула:

,

Выразив Rполучим и подставив численные значения Q, L и C найдем R=0,173 Ом.

4.2.1 Комплексный частотный коэффициент передачи колебательного звена

Найдем математическое выражение для комплексного частотного коэффициента передачи, исходя из схемы приведенной на рисунке 4.6:

. (4.8)

Из формулы (4.8), как и для апериодического звена, можно легко получить АЧХ и ФЧХ колебательного звена.