Лабораторная работа: Амплитудная модуляция смещением

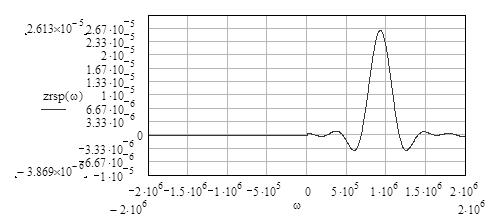
Рисунок 3.8 - Спектральная плотность аналитического сигнала

3.5 Дискретный сигнал, соответствующий видеосигналу

В соответствии с теоремой Парсеваля полная энергия сигнала равна:

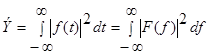, (3.20)

Ограничим спектр исходного видеосигнала некоторой граничной частотой f_g , таким образом, что бы энергия сигнала, с «ограниченным спектром» была равна 99% энергии исходного сигнала. Находим граничную частоту по формуле, из условия:

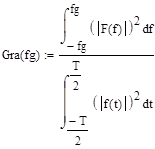, (3.21)

Получаем f_g »63,2 кГц.

Если теперь считать, что сигнал имеет спектр, наивысшая частота которого равна f_g , то в соответствии с теоремой Котельникова, сигнал может быть полностью определен дискретными выборками, взятыми с частотой 2f_g , называемой частотой дискретизации.

Найдем интервал дискретизации T_d :

, (3.22)

Математическую модель дискретного f_d (n) сигнала можно записать в следующем виде:

, (3.23)

где

n,k – целые числа;

f(kT_d ) – выборки из видеосигнала (3.2) кратные интервалу дискретизации;

d(n) – единичный импульс определенный как:

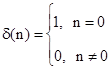, (3.24)

Графическое изображение дискретного сигнала f_d (n) приведено на рисунок 3.9.

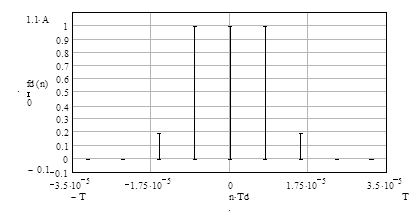
Рисунок 3.9 - Дискретный сигнал

Для отыскания спектральной плотности дискретного сигнала воспользуемся соотношением:

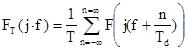, (3.25)

где 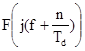- спектральная плотность видеосигнала (3.5) на соответствующих частотах.

Модуль спектральной плотности дискретного сигнала приведен на рисунок 3.10.

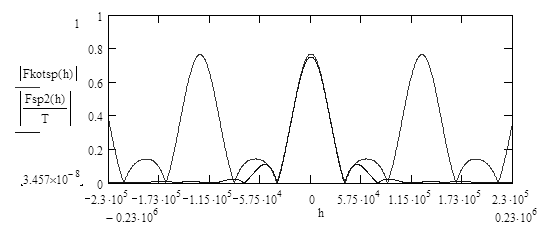
Рисунок 3.10 - Модуль спектральной плотности дискретного сигнала, модуль спектральной плотности видеосигнала.

Таким образом, спектр дискретного сигнала периодичен по частоте, с периодом равным частоте дискретизации. Если эффект наложения спектров отсутствует, то в полосе частот от минус половина частоты дискретизации до плюс половина частоты дискретизации, спектр дискретного сигнала равен спектру аналогового сигнала. Для случая приведенного на рисунок 3.11 это условие не выполняется. Поэтому восстановленный сигнал будет искажен рисунок 3.11.

3.6 Сигнал представленный рядом Котельникова

Получить сигнал, определенный в любой момент времени (аналоговый сигнал f_a (t)) можно используя интерполяционную формулу: