Реферат: Алгебраические уравнения с одной неизвестной и способы их решения в основной школе

Покажем, как решаются неполные квадратные уравнения.

1. Уравнение имеет единственный корень .

2. Уравнение равносильно уравнению . Возможны два случая.

Если , то , и поэтому уравнение не имеет действительных корней.

Если , то , и уравнение имеет два корня: , .

Действительно, перенося в уравнении величину в левую часть, получаем .

Так как , то . Поэтому .

Разложив левую часть этого уравнения на множители, получим .

Данное произведение равно нулю, если хотя бы один из сомножителей равен нулю.

Рассматривая , получим ; рассматривая , находим .

Следовательно, уравнение при имеет два корня; , что и утверждалось. Ответ часто записывается в виде .

Например, неполное квадратное уравнение не имеет действительных корней. Для неполного квадратного уравнения по­лучаем

Это уравнение можно решить по-другому:

3. Уравнение можно решить с помощью разложения его левой части на множители. Очевидно, что , откуда , . Например, , откуда , .

В общем случае для решения квадратных уравнений применяется метод выделения полного квадрата. [5, c.120]

Применение этого метода поясним сначала на примерах.

Пример 1. Решить квадратное уравнение

Решение. Разделим обе части уравнения на :

.

Применим метод выделения полного квадрата: .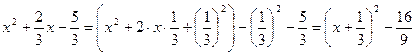

Поэтому получим

,

откуда . Следовательно,

, .

Можно выделить полный квадрат в исходном уравнении и без предварительного деления на (коэффициент при квадрате неизвестного):

.
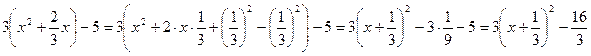