Реферат: Алгебраические уравнения с одной неизвестной и способы их решения в основной школе

и т.д. [2, c.107]

Рассмотрим теперь квадратное уравнение общего вида

. (1)

Применим метод выделения полного квадрата. Для этого запишем левую часть уравнения в следующем виде:

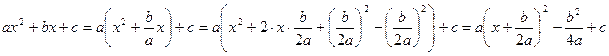.Поэтому

или . (2)

Дальнейшее решение зависит от знака правой части полученного уравнения (2).

Так как , то знак правой части совпадает со знаком выражения . [15, c.163]

Определение. Выражение называется дискриминантом квадратного уравнения и обозначается буквой : .

Рассмотрим три случая: .

1. .

В этом случае уравнение (2) можно записать так:

;

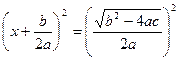следовательно,

,

откуда

, (3)

или

, (4)

где - дискриминант уравнения (1).

Таким образом, в случае положительного дискриминанта, т.е. при , уравнение имеет два различных корня, которые можно найти по формуле (3) или (4).

2. .

В этом случае уравнение (2) принимает вид

,

откуда , т.е. .

Таким образом, если дискриминант равен нулю, т.е. , то уравнение имеет единственный корень .

Заметим, что формула (3) или, что то же, (4) применима и в случае . В самом деле, эта формула дает единственный корень уравнения (1). Говорят также, что в этом случае квадратное уравнение имеет два равных корня: . Такое соглашение освобождает нас от специальных оговорок, относящихся к этому случаю при формулировке свойств квадратных уравнений.

3. .

В этом случае в правой части уравнения (2) стоит отрицательное число, а в левой части - неотрицательное (положительное или равное нулю). Следовательно, если , то уравнение (2), а значит, и уравнение не имеют действительных корней.