Реферат: Алгебраические уравнения с одной неизвестной и способы их решения в основной школе

По этой формуле можно находить и корни неполных квадратных уравнений, но проще вычислять их путем разложения левой части неполного квадратного уравнения на множители, как было показано.

Замечание 1. Если коэффициент - четное число, т.е. , то формула корней квадратного уравнения примет вид

. [2, c.114]

Например, вычислим корни уравнения (заметим, что уравнение имеет действительные корни, так как ):

.

Замечание 2. Если коэффициент , то квадратное уравнение принимает вид . Такое квадратное уравнение называется приведенным квадратным уравнением. Всякое квадратное уравнение можно привести к виду делением обеих частей уравнения на . [2, c.117]

Найдем корни приведенного квадратного уравнения. В формуле (3) полагаема . Тогда

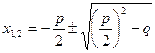- формула корней приведенного квадратного уравнения .

Например, решим уравнение :

,

Откуда

Пример 2. Решить уравнение .

Решение. Разложив знаменатели на множители, имеем

.

После приведения дробей к общему знаменателю получим уравнение или , равносильное исходному уравнению, при условии, что , т.е. , . Находим корни приведенного квадрат­ного уравнения:

,

откуда , . Так как не удовлетворяет ограничению (не входит в ОДЗ исходного уравнения), то, следовательно, исходное урав­нение имеет единственный корень . [2, c.124]

Теорема Виета. Если квадратное уравнение имеет действительные корни и , то их сумма равна и произведение равно :

, . (5)

Формулы (5) называются формулами Виета.

Доказательство. По условию дискриминант квадратного уравнения . Тогда по формуле (4) уравнение имеет два корня:

, .

Найдем сумму и произведение корней:

,

,

и формулы (5) получены.

Теорема Виета устанавливает связь между корнями квадратного уравнения и его коэффициентами.

Для приведенного квадратного уравнения с дискриминантом формулы (5) принимают вид

, . (6)

Полученные для приведенного квадратного уравнения формулы Виета читаются так: сумма корней приведенного квадратного уравнения равна коэффициенту при неизвестном в первой степени, взятому с противоположным знаком, а произведение корней равно свободному члену.