Реферат: Аналитическая геометрия

r=sqrt((x-p/2)² +y² ); d=p/2+x

Приравниваем и получаем:

y² =2px - каноническое уравнение параболы

ЭКСЦЕНТРИСИТЕТ И ДИРЕКТРИСА ЭЛЛИПСА И ГИПЕРБОЛЫ.

1. Определение: эксцентриситет – величина равная отношению с к а.

е=с/а

е эллипсв <1 (т.к. а>c)

е гиперболы >1 (т.к. с>a)

Определение: окружность – эллипс у которого а=b, с=0, е=0.

Выразим эксцентриситеты через а и b:

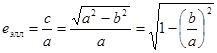
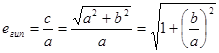
е эллипса является мерой его “вытянутости”

е гиперболы характеризует угол раствора между асимптотами

2. Директрисой D эллипса (гиперболы), соответствующей фокусу F, называется прямая расположенная в полуплоскости a перпендикулярно большой оси эллипса и отстоящий от его центра на расстоянии а/е>a (а/е<a)

D₁ : x= - a/e

D₂ : x= a/e

р=а(1-е² )/е – для эллипса

р=а(е² -1)/е – для гиперболы

ТЕОРЕМА ОБ ОТНОШЕНИИ РАССТОЯНИЙ. 2-ОЕ ОПРЕДЕЛЕНИЕ ЭЛЛИПСА, ГИПЕРБОЛЫ, ПАРАБОЛЫ.

Теорема: Отношение расстояния любой точки эллипса (гиперболы) до фокуса к расстоянию от нее до соответствующей директрисы есть величина постоянная равная е эллипса (гиперболы).

Доказательство: для эллипса.

r₁ /d₁ =e

x£|a|, xe+a>0

r₁ =xe+a

d₁ – расстояние от М(x,y) до прямой D₁

xcos180+ysin180-p=0

x=-p

x=-a/e