Реферат: Аналитическая геометрия

Пусть I₃ <0

-(-а₁₁ ’’)x’’² +a₂₂ ’’ y’’² = -I₃ /I₂

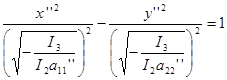
В этом случае мы имеем гиперболу с действительной осью ОY

Пусть I₃ =0

а₁₁ ’’x’’² -(-a₂₂ ’’)y’’² =0

АСИМПТОТИЧЕСКИЕ НАПРАВЛЕНИЯ КРИВЫХ 2-ГО ПОРЯДКА.

Пусть крива второго порядка задана уравнением (1). Рассмотрим квадратную часть этого уравнения: u(x,y)= a₁₁ x² +2a₁₂ xy+a₂₂ y²

Определение: ненулевой вектор (a, b) координаты которого обращают в ноль квадратичную часть называется вектором асимптотического направления заданной кривой.

(a, b) – вектор асимптотического направления.

a₁₁ a² +2a₁₂ ab+a₂₂ b² =0 (*)

Рассмотрим (a’, b’) параллельный (a, b): следовательно . Дробь a/b характеризует вектор асимптотического направления.

Задача: выяснить какие асимптотические направления имеют кривые 2-го порядка.

Решение: положим, что b¹0 и поделим на b² , получим: a₁₁ (a/b)² +2a₁₂ a/b+a₂₂ =0 из этого квадратного уравнения найдем a/b.

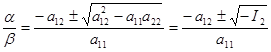
т.к. у линий гиперболического и параболического типов I₂ £0, то они имеют асимптотические направления. Т.к. у эллипса I₂ >0 следовательно таких у него нет (говорят он имеет мнимые асимптотические направления).

Найдем асимптотические направления у гиперболы:

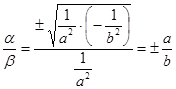
(a, b)₁ =(a,b)

(a, b)₂ =(-a,b)

Векторы асимптотического направления являются направляющими векторами для асимптот.

Итак: гипербола имеет два асимптотических направления, которые определяются асимптотами гиперболы.

Найдем асимптотические направления у параболы:

y² =2px

y² -2px=0

u(x,y)= y² +0, y=0

(a, b)=(0,0)