Реферат: Аналитическая геометрия

a₁₁ x’² +2a₁₂ x’y’+a₂₂ y’² +a’₃₃ =0 (2)

точка О’ находится из условия: a₁₃ ’=0 и a₂₃ ’=0.

Получается система a₁₁ x₀ +a₁₂ y₀ +a₁₃ =0 и a₁₂ x₀ +a₂₂ y₀ +a₂₃ =0

Покажем, что новое начало координат (если система разрешима) является центром симметрии кривой: f(x’;y’)=0, f(-x’;-y’)= f(x’;y’)

Но точка О’ существует если знаменатели у x₀ и y₀ отличны от нуля.

Точка O’ – единственная точка.

Центр симметрии кривой существует если I₂ ¹0 т.е. центр симметрии имеют линии элиптического и гиперболического типа

Поворот:

Пусть система XOY повернута на угол u. В новой системе координат уравнение не содержит члена с x’y’ т.е. мы делаем коэфф. а₁₂ =0. a₁₂ ’= -0,5(a₁₁ -a₂₂ )sin2u+a₁₂ cos2u=0 (разделим на sin2u), получим:

, после такого преобразования уравнение принимает вид

a₁₁ ’x’² +a₂₂ ’y’² +2a₁₃ ’x’+2a₂₃ ’y’+a₃₃ ’=0 (3)

ТЕОРЕМА О ЛИНИЯХ ЭЛИПТИЧЕСКОГО ТИПА.

Теорема: Пусть задана линия элиптического типа т.е. I₂ >0 и пусть I₁ >0следовательно уравнение (1) определяет: 1. I₃ <0 – эллипс; 2. I₃ =0 – точка; 3. I₃ >0 – ур-е (1) не определяет. Если I₃ =0 говорят, что эллипс вырождается в точку. Если I₃ >0 говорят, что задается мнимый эллипс. Пусть после ПП и поворота ур-е (1) принимает вид (*).

Доказательство:

1. пусть I₂ >0, I₁ >0, I₃ <0, тогда

а₁₁ ’’x’’² +a₂₂ ’’ y’’² = -I₃ /I₂

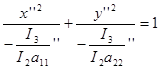
I₂ =a₁₁ ’’a₂₂ ’’ > 0

I₁ = a₁₁ ’’+a₂₂ ’’ > 0

a₁₁ ’’ > 0; a₂₂ ’’ > 0

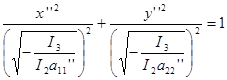
Итак, под корнями стоят положительные числа, следовательно, уравнение эллипса.

2. I₃ >0 в данном случае под корнем стоят отрицательные числа, следовательно уравнение не определяет действительного геометрического образа.

3. I₃ =0 в данном случае т(0,0) – случай вырождения эллипса.

ТЕОРЕМА О ЛИНИЯХ ГИПЕРБОЛИЧЕСКОГО ТИПА.

Теорема: Пусть уравнение (1) определяет линию гиперболического типа. Т.е. I₂ <0, I₃ ¹0 - ур-е (1) определяет гиперболу; I₃ =0 – пару пересекающихся прямых.

Доказательство: I₂ <0; I₂ = a₁₁ ’’a₂₂ ’’ < 0. Пусть a₁₁ ’’>0; a₂₂ ’’<0

Пусть I₃ >0