Реферат: Численное решение краевых задач для двумерного уравнения колебания

В этом случае обращается диагональная матрица, требующая лишь 0(N) арифметических операций.

Условием устойчивости схемы (2.4)-(2.6) будет

Отсюда видно, что условием устойчивости явной схемы будет

Из условия (2.7) видно, что схемы о , в том числе чисто неявная схема при и симметричная схема при , абсолютно устойчивы.

Если имеем уравнение с переменными коэффициентами, т.е.

(2.8)

то

Условие устойчивости схемы (2.4)-(2.6) с эллиптическим оператором (2.8) имеет вид

Отсюда получаем условие устойчивости явной схемы в виде

(2.9)

Условие устойчивости (2.9) налагает весьма жесткие огра­ничения на шаг по времени и выход на заданный момент време­ни по явной схеме требует неоправданно большого числа вре­менных шагов.

Из условия (2.9) видно, что выбор шага существенно за­висит от количества пространственных переменных р и от вели­чины М. С ростом числа р и для быстро меняющегося коэффици­ента теплопроводности K=K(x,t) шаг становится еще мель­че. В этом случае схема (2.4)-(2.6) при становится неэф­фективной, так как выход на заданный момент времени t=T тре­бует слишком большого числа временных шагов.

Чисто неявная схема () (2.4)-(2.6) абсолютно устойчива, т.е. на параметры сетки h и не налагаются ограничения. Поэтому счет можно вести более крупными шагами hи и тем самым удается значительно понизить порядок системы, уменьшить количество временных шагов, необходимых для достижения момента времени t = Т .

В неявных схемах придется решать системы алгебраических уравнений, как правило, высокого порядка и с разреженными матри­цами. Итак, реализация систем алгебраических уравнений для мно­гомерных задач в общем случае представляется невозможной из-за громоздкости порядка системы (проблема памяти ЭВМ), большого объема арифметических операций.

Таким образом, лучшими качествами явной и неявной схем являются количество арифметических операций, равное 0(N) в явной схеме, и абсолютная устойчивость неявной схемы, недостат­ками - условная устойчивость явной схемы и большое количество арифметических операций в неявной схеме. Отсюда ясно, что если построим разностные схемы, сочетающие в себе лучшие качества обычных явных и неявных разностных схем, то можно эффективно решать многомерные задачи математической физики.

Итак, безусловная (абсолютная) устойчивость и независимость количества арифметических операций, требуемые для вычисления приближенного решения задачи в отдельной точке сетки от общего количества узлов сеточной области, определяют класс экономичных схем.

Уравнение (2.1) можно аппроксимировать по-другому, стремясь упростить вычислительный процесс. Уравнение (2.1) аппроксимируем разностным уравнением

В этой схеме аппроксимация по первому направлению неявная, а по всем остальным - явная.

Реализация этой схемы идет по направлению , как в од­номерном случае методом линейной прогонки, затратой арифметичес­ких операций порядка . Однако схемы (2.10), (2.5), (2.5) условно устойчивы. Таким образом, из требований экономичности разностной схемы первое условие не выполнено, а второе - выпол­нено. Поэтому схемы типа (2.10), (2.5), (2.6) не относятся к классу экономичных схем, они конструируются специальным образом.

2. Достижением вычислительной математики является разра­ботка экономичных методов решения многомерных краевых задач ма­тематической физики. Первые экономичные схемы были схемами в дробных шагах по времени t. Они предложены и обоснованы в 1955 г. одновременно американскими учеными D.W. Peacemdn , H.H.Rachford и J.Douglas.

Характерной особенностью экономичных схем этого периода является то, что все они основывались на идее ведения дробных моментов времени и поэтапном решении р задач в промежутках . Решением исходной задачи будет решение последней р -й задачи в момент времени . Решения осталь­ных (р-1) задач являются вспомогательными в моменты времени . Таким образом, наряду с основной сеткой по рассматривается вспомогательная сетка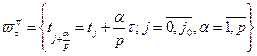. Все эконо­мичные схемы этого периода относятся к схемам последовательного перехода по времени t. Следуя Н. Н. Яненко, назовем их ме­тодом дробных шагов.

В 1965г. А. А. Самарский предложил и обосновал экономичный метод без привлечения вспомогательной сетки , т.е. экономичная схема конструируется на исходной сетке . Таким образом, характерной областью экономичных схем этого периода является то, что сетка не вводится, вспомогательные функции рассматриваются на верхнем слое. Составная схема конструируется на исходной сетке